模型量化原理与实践

December 17, 2023

本文主要介绍深度学习神经网络模型的量化原理和工程实践，主要包括如下内容：

基本原理：量化映射、量化粒度、量化计算、算子融合等；
模型量化方法：权重\激活量化、PTQ、QAT等；
工程实践：PyTorch 模型量化介绍&示例；
工程实践：高通 QNN 量化工具介绍&示例；
LLM 量化算法简介；

一、基本原理

量化简介

神经网络的计算通常以浮点计算(FP32)进行，而量化则是将浮点计算替换为更低比特的计算，如 FP16、INT8 等，从而降低模型的存储大小、降低显存占用、提升推理性能，当然，量化的同时需要尽可能保持模型的精度，因此需要设计合适的量化方案。

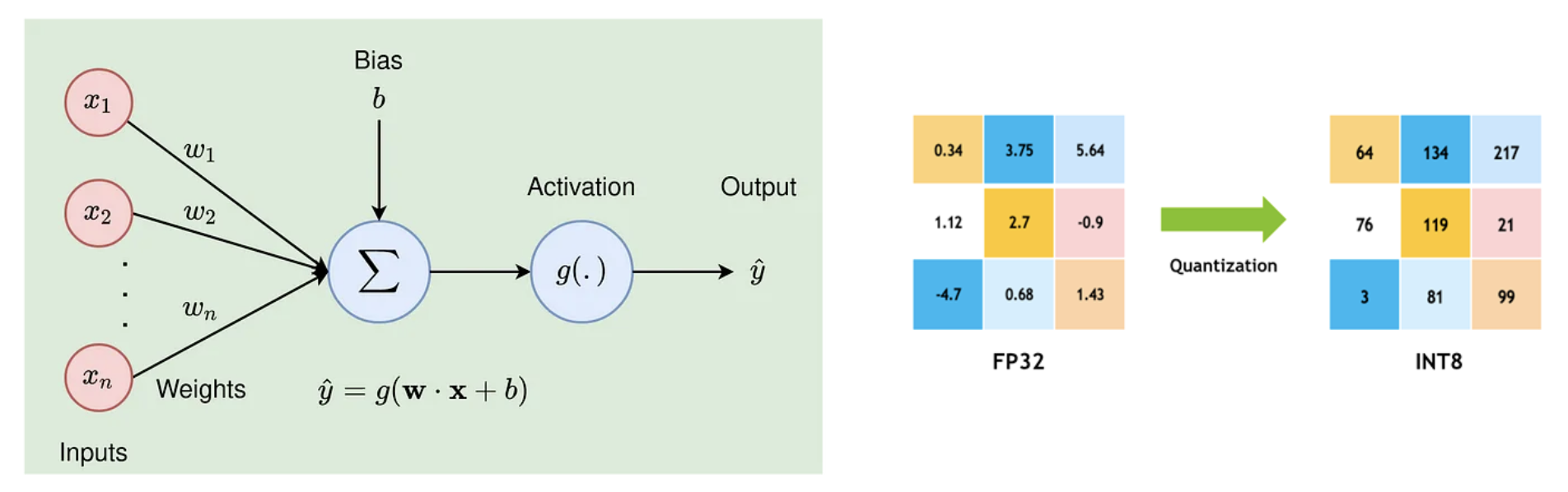
量化映射

数值的量化可以看作一个近似过程，主要可分为两类：

Fixed Point Approximation

定点近似主要是缩小浮点表示中的指数和小数部分的位宽，不需要额外的量化参数，也没有反量化过程，实现相对简单，但是在数值较大时，直接定点近似会带来较大的精度损失。
Range Based Approximation

基于范围的近似，则是先统计待量化数据的分布，然后进行整体的缩放和偏移，再映射到量化空间，精度相对更高，但需要额外存储量化参数(如缩放系数、偏移等)，并且计算时需要先反量化，比定点近似更复杂。根据映射方式的不同，又可分为线性映射和非线性映射：

线性映射

线性映射将数值从浮点空间线性变换到量化空间，可用如下公式表示：

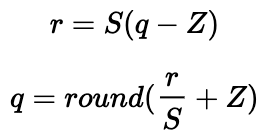
其中 r、q 分别是量化前、后的数，S (Scale)和 Z (Zero-Point)是量化系数，Z 有时也称为偏移(Offset)，可以看作是原数值 0 量化后的值，根据 Z 是否为 0，线性映射又可分为对称映射和非对称映射：

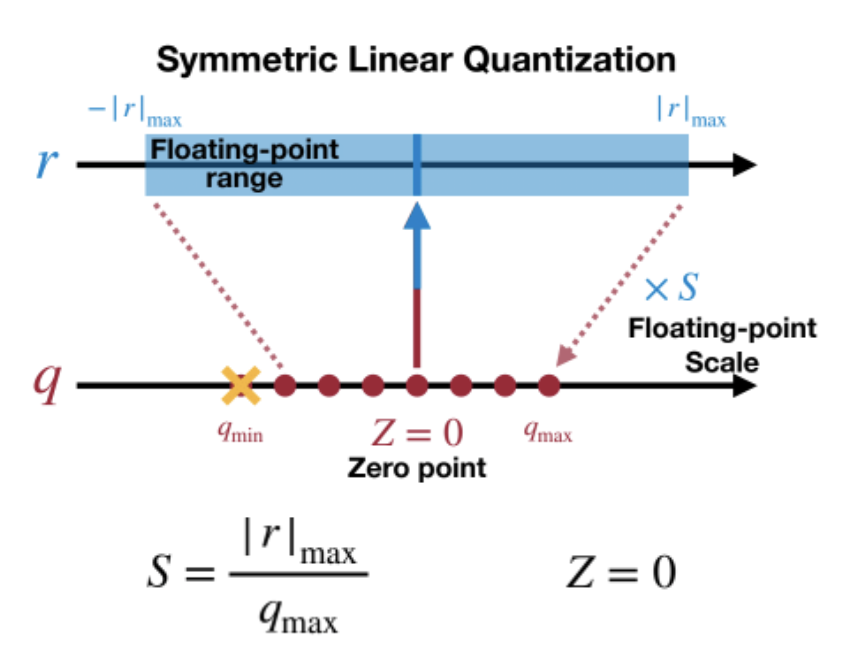
如上图，对称映射的 Z 始终为 0，即原数值的 0 量化后仍然是 0，量化前后的数值都是以 0 为中点对称分布，但实际上有些数值的分布并不是左右对称的，比如 ReLU 激活后都是大于 0，这样会导致量化后 q 的范围只用到了一半，而非对称映射则解决了这个问题：

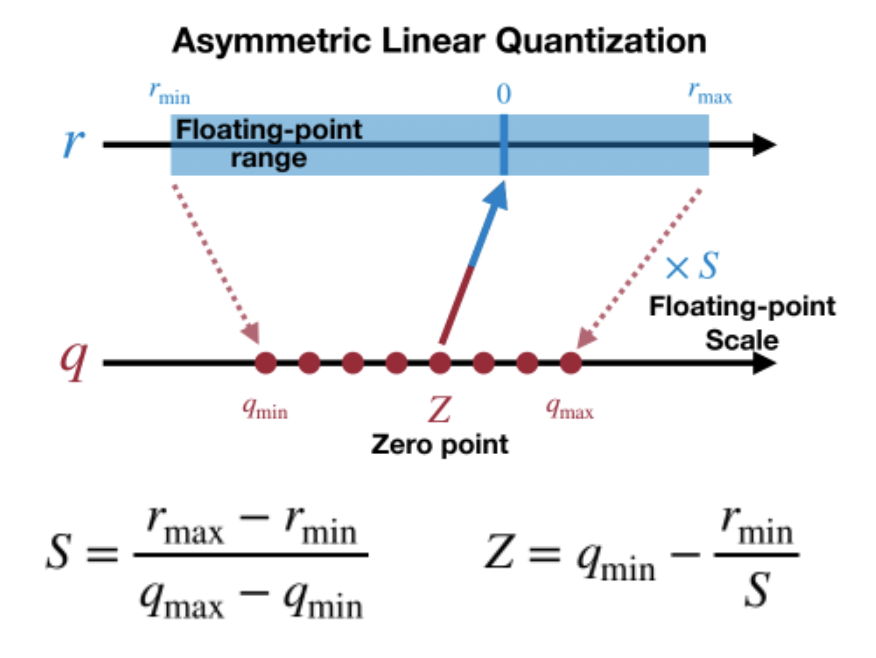
非对称映射的 min、max 独立统计，Z 的值根据 r 的分布不同而不同，这样可以使 q 的范围被充分利用。

我们来看一个实际的例子：量化 FP32 [-1.8, -1.0, 0, 0.5] 到 INT8 [0, 255] (非对称)：

r_min = -1.8，r_max = 0.5， bitWidth = 8
S = (r_max – r_min)/(q_max – q_min) = (0.5 – (-1.8)) / (255 – 0) = 0.009019607843
Z = q_min – r_min/S = 0 – (-1.8)/S = 199.56521739 ≈ 200
量化结果：q = round([-1.8, -1.0, 0, 0.5] / S + Z) = [0, 89, 200, 255]

反量化：

r’ = S * ([0, 89, 200, 255] – Z) = [-1.80392157, -1.00117647, 0, 0.49607843]

可以看到：反量化后数值对比原始数值存在一定误差。

非线性映射

量化是一个数值映射过程：[r0, r1, …,rk] -> [q0, q1, …, qk] ，对于线性映射，并没有考虑原始数据本身的分布，如下图的正态分布，越靠近中间的 0，数据分布越密，左边是线性映射，量化后数值也同样会集中在中间的 0 附近，如果更极端一点，会导致大量的数值量化后都是 0，显然这样就降低了量化的精度，而如果按右图，对数据分布密集的区域，给与更多的量化映射，就能增加量化后的差异性，提高精度。实际上，我们希望量化后的数据在量化空间应该均匀分布，而不是被原始数据的分布所影响。

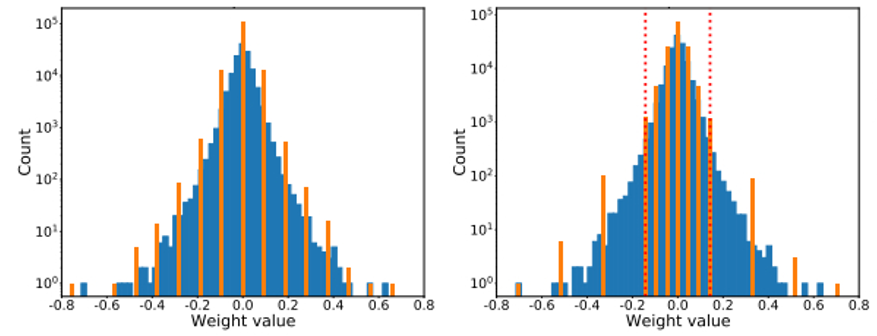
非线性映射有多种实现，这里介绍一种分位量化方法（Quantile Quantization）：分位量化的基本想法是寻找一些分位点对原数据进行划分，使得各个区间的数据个数相等，然后将同一个区间的数据映射到同一个值，从而实现了量化。

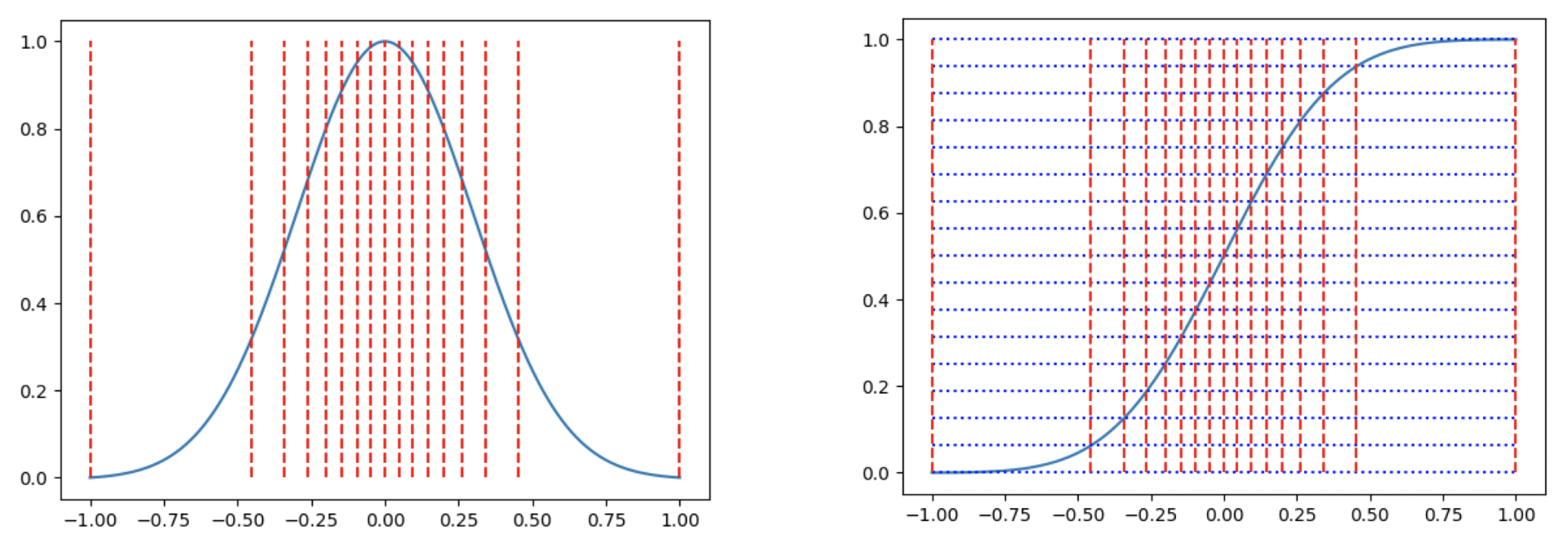
如上图左边是一个类似于标准正态的分布图，红色竖线是16等分的分隔线，即相邻的分隔线截取的曲线面积相等，这样我们再把区间中的数都用区间中点来映射，即完成了分位量化，那如何求这些分隔线的位置呢？可以用累积分布函数的反函数来计算，如上图右图，累计分布函数(CDF)可以看作是左图积分图，我们把纵坐标进行16等分，那么等分线与CDF曲线的交点对应的横坐标即为分位点，我们用 Q_x 表示CDF函数的反函数，q_i 表示各个区间的中点，Q^map 是所有 q_i 的集合，Q^map = [q₀, q₁, … q_2^k-1]，则有：

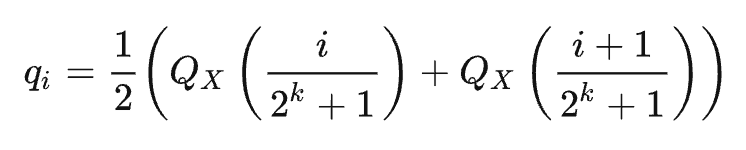
实际计算过程中，需要先将数据归一化到合适的范围，并且对于确定的分布来说，分位点也是确定的，因此只需存储分位点的索引即可，整体步骤如下：

计算归一化常数 N=max(|T|) ，将输入张量T转化到目标量化数据类型的范围内
Q^map 是 q_i 的集合，对于T/N的每个元素，搜索在 Q^map 中最接近的对应值q_i
将对应 q_i 的索引 i 作为量化输出结果

LLM QLoRA 算法提出的 NF4(4-bit NormalFloat Quantization) 是分位量化的一种实现，其采用 4 bit，总共有16个分位数，并且为了保持 0 映射后仍然是 0 进行了特殊处理，把[-1, 0]分成7份，然后生成[-1, …, 0]共8个分位数, 把[0, 1]分成8份，然后生成[0, …, 1]共9个分位数，两个合起来去掉一个0就生成全部的16个分位数：

Q_map = [-1.0,                 -0.6961928009986877,  -0.5250730514526367,  -0.39491748809814453,
         -0.28444138169288635, -0.18477343022823334, -0.09105003625154495,  0.0,
          0.07958029955625534,  0.16093020141124725,  0.24611230194568634,  0.33791524171829224,
          0.44070982933044434,  0.5626170039176941,   0.7229568362236023,   1.0]

NF4 量化的16个区间分布如下图，各区间的面积基本相当，整体上也是符合正态分布的：

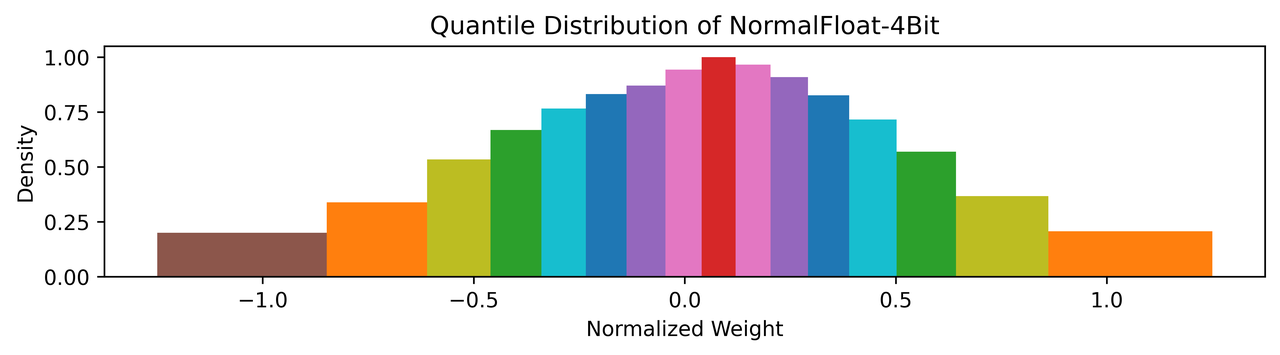
具体来看一个 NF4 量化的例子：

原始输入数据：[-5, 3, 16, 8]
计算归一化常数 N = max{abs(x_i)} = 16
将输入数据归一化到 [-1, 1]：[-5, 3, 16, 8] / N = [-0.3125, 0.1875, 1.0, 0.5]
从Q^map找到最接近的分位数q_i, 将索引作为量化结果：[4, 9, 15, 12]

可以看到，量化之后需要存储的是归一化常数 N 和 q_i 的索引，接下来是反量化：

将量化结果作为索引从Q^map中找到对应分位数[4, 9, 15, 12] -> [-0.28444138169288635, 0.16093020141124725, 0.7229568362236023, 0.33791524171829224]
将分位数反归一化(乘以N)：[-4.551062107, 2.574883223, 16, 7.051357269]

量化粒度

量化粒度指选取多少个待量化参数共享一个量化系数，通常来说粒度越大，精度损失越大，比如下面5个数一起量化到[0, 255]，由于存在一个离群值(outlier) 1000，导致前面四个数量化后都是 0，失去了差异性，从而影响结果的精度。

[-1.8, -1.0, 0, 0.5, 1000] -> [0, 0, 0, 0, 255] -> [0, 0, 0, 0, 1001.8]

再看一个例子，如下四个数 [100, 90, 0.3, 0.1]，如果4个数一起量化，最终误差为 0.64，而如果分为两组分别量化，则最终误差只有 0.241，从这里也可以看出，通过将值域范围接近的数分组量化，能降低量化误差。

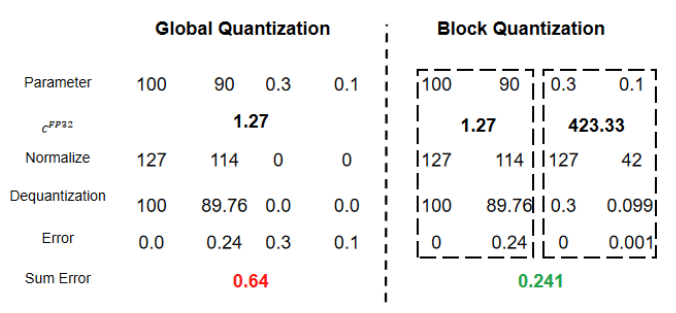
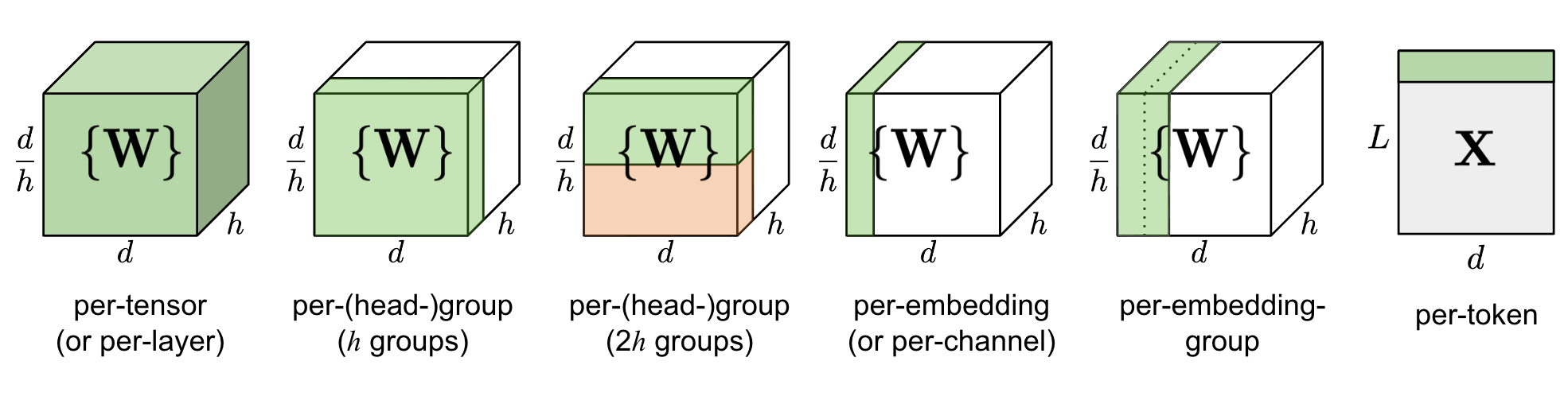
根据分组的依据不同，量化粒度有多种形式：

per-tensor/per-layer
per-channel/per-axis
per-col/per-row
per-embeding/per-token
per-block/group

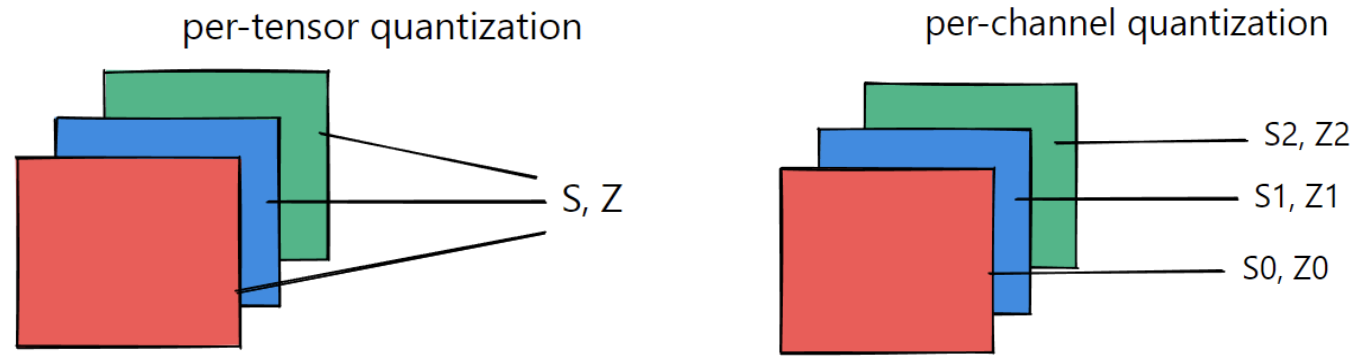
一般来说，量化粒度越小，需要额外存储的量化系数就越多，比如针对卷积运算常见的 per-tensor/per-channel 量化，如下图所示，per-tensor 只需一组 (S, Z) 量化系数，而 per-channel 需要多组，提升了量化精度，但同时会一定程度增加量化后数据的大小

量化计算

硬件的整型/定点计算通常比浮点计算更快，因此量化到整型/定点后，有利于推理性能的提升，接下来看看常用的算子在量化后有什么区别，首先是最基本的加、乘：

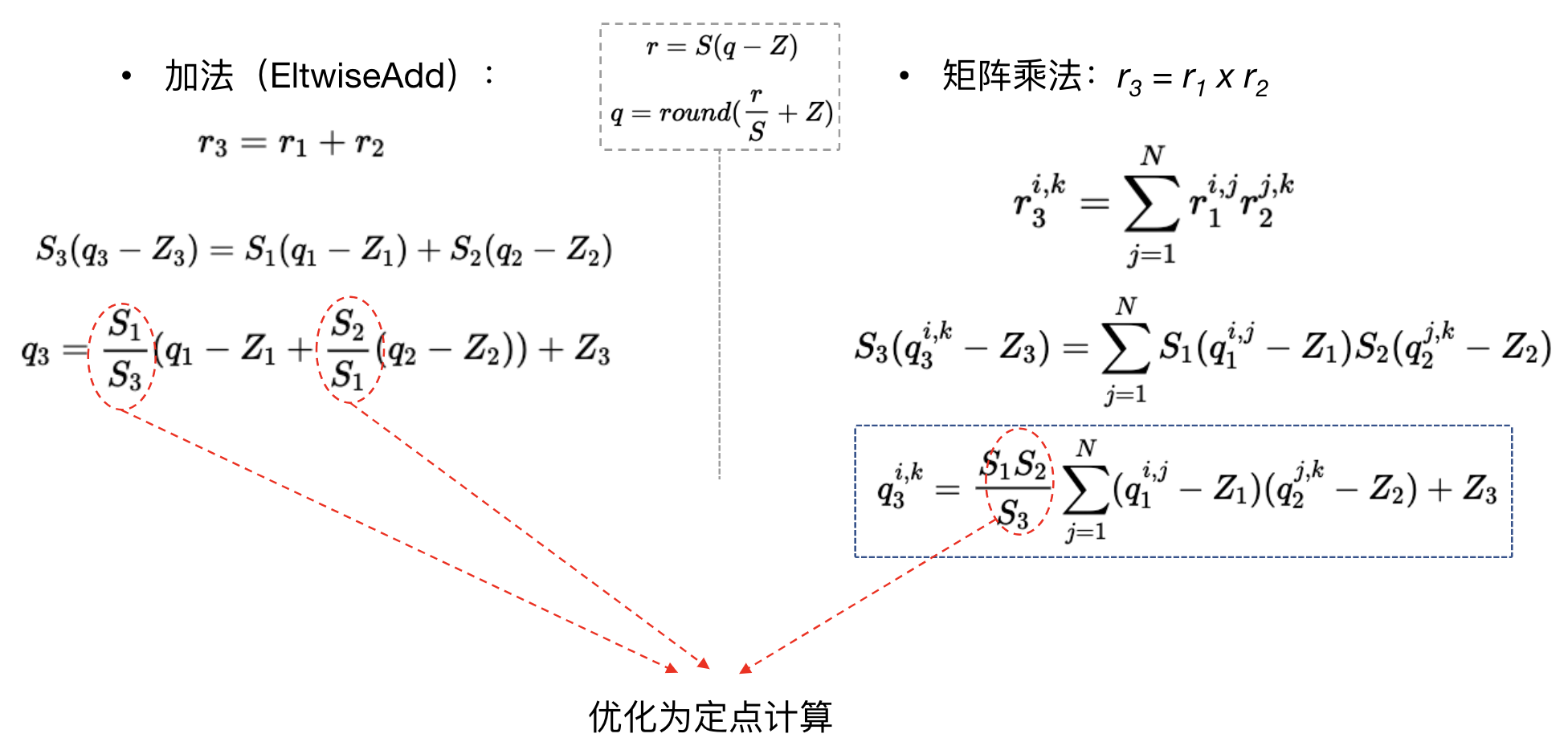
可以看到，线性量化后，q、z 相关的都是整型计算，但仍然会有量化系数 S(FP32)的计算，这部分(图中红圈)也可以优化为定点计算来提升速度：

我们将浮点数用 Q 表示法转换为定点数：

q_fixed = (int) (x_float * 2^Q)
x_float = (float) (q_fixed * 2^-Q)

这样两个浮点数 x1、x2 的乘法可以展开为：

x1 x2 = (q1 2^-Q) (q2 2^-Q) = (q1 q2) 2^-2Q = ((q1 q2) >> Q) 2^-Q

即最终只有整型的乘法(q1 * q2)和移位操作，举个例子：

0.234 * 0.84 = 0.19656，取 Q = 30
0.234 ≈ 251255586 * 2^-30
0.84 ≈ 901943132 * 2^-30
251255586 * 901943132 = 226618250169335352 (注意这里需要使用64位乘法，避免溢出)
226618250169335352 >> 30 = 211054692

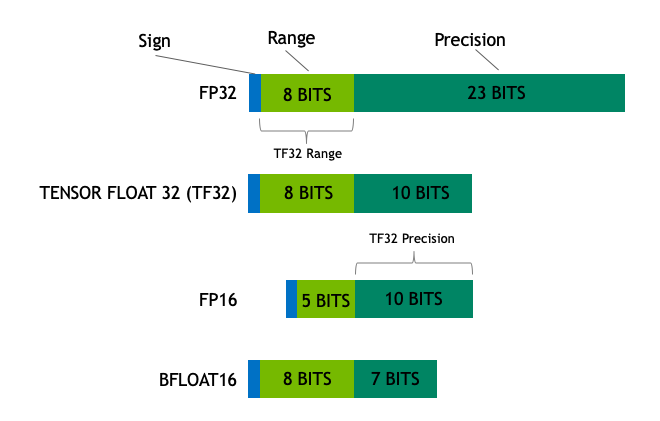
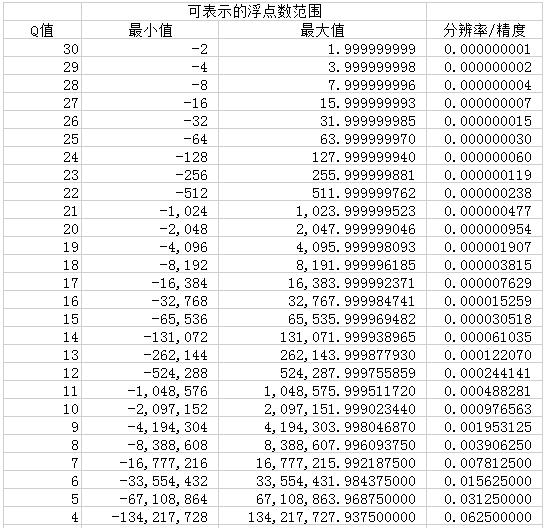
即计算结果为： 211054692 2^-30 ，转换为浮点数：211054692 2^-30 = 0.19655999913 ，可以看到精度是比较高的，这里 Q 取值越大，精度越高，但可表示范围也越小，如下表所示：

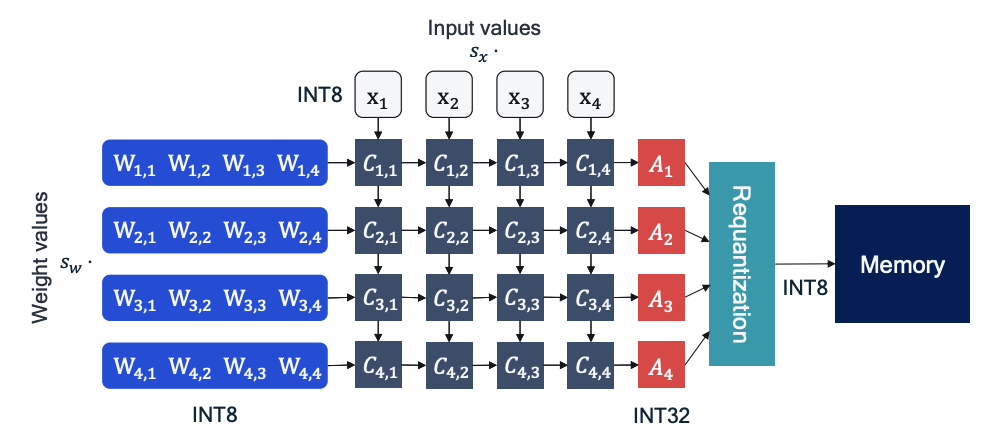
下图是卷积运算的硬件实现示意图：可以看到 A₁、A₂、A₃、A₄ 都是 INT32，即用更高的位宽来存储中间结果，避免溢出，然后再重新量化为 INT8，这里的 requantization 可以合并一些后续的激活操作（如 ReLU），进一步提升推理性能。

对于一些较复杂的激活函数，通常是非线性的，量化计算主要有查表法和拟合法两类。查表法实现相对简单：对于低比特量化，x可取值总数有限，可以提前计算好映射表(如INT8的表长为256)，推理时直接从表中取值即可：

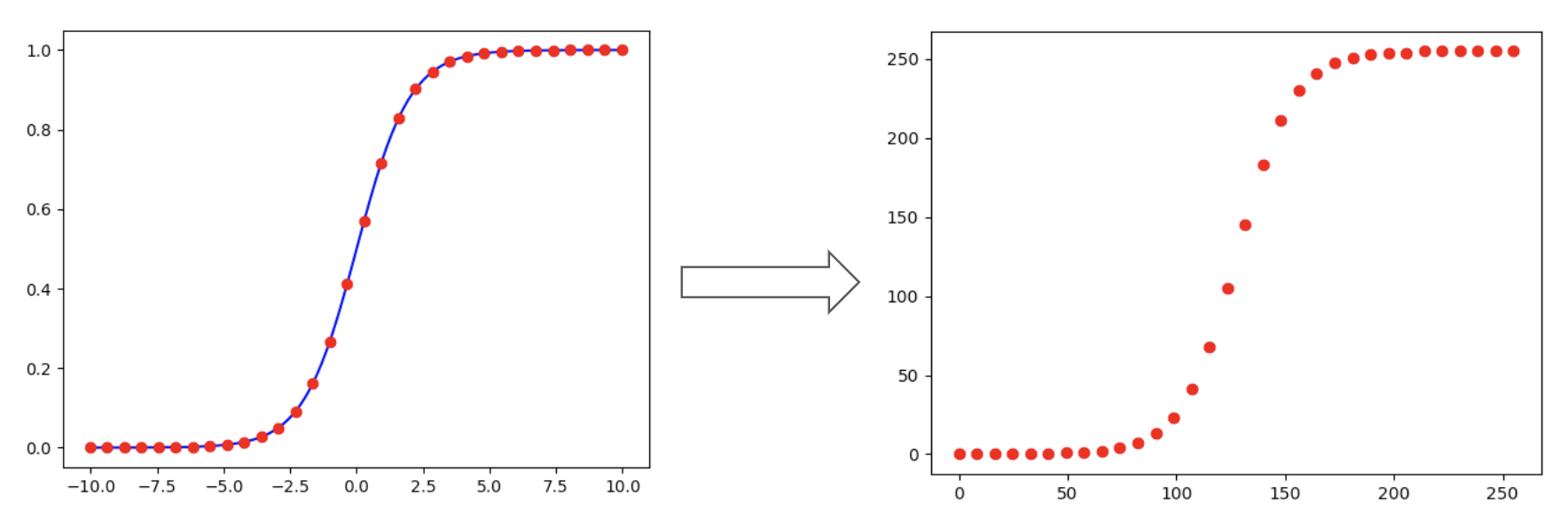
而拟合法则是通过使用多相似逼近、泰勒展开等方式，用低阶函数来模拟，比如 GELU 激活中的 erf 函数，通过一个二次函数 L(x) 来拟合：选取一些采样点，然后用最小二乘法，计算得到 a = -0.2888, b = -1.769, c = 1，右边是 erf 函数真实点与拟合曲线的示意，可以看到拟合精度还是不错的。

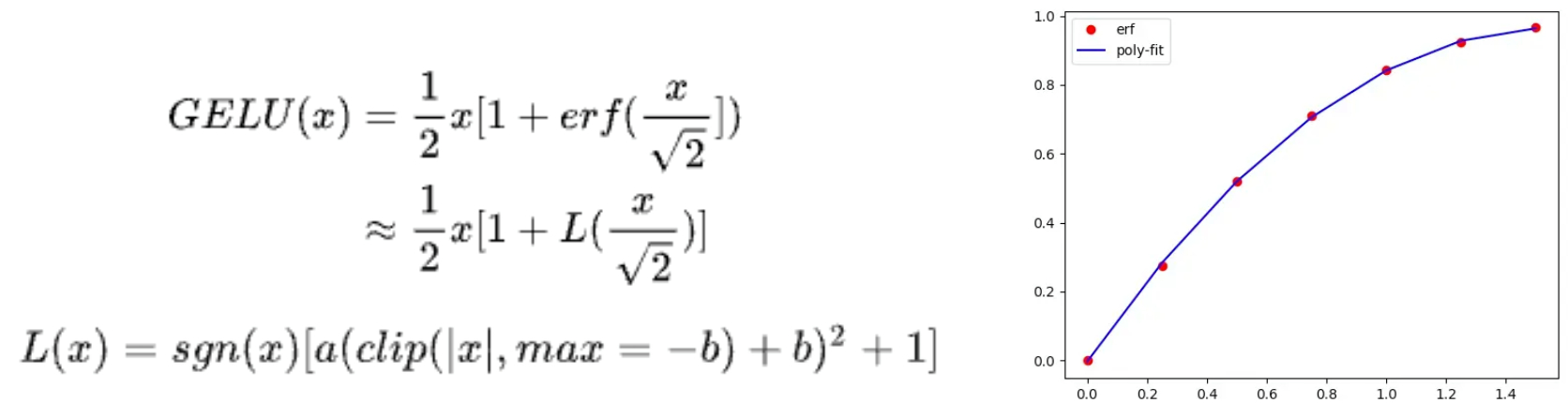
同样的对于 SoftMax 中的 exp，也可以同样的进行二项式拟合：

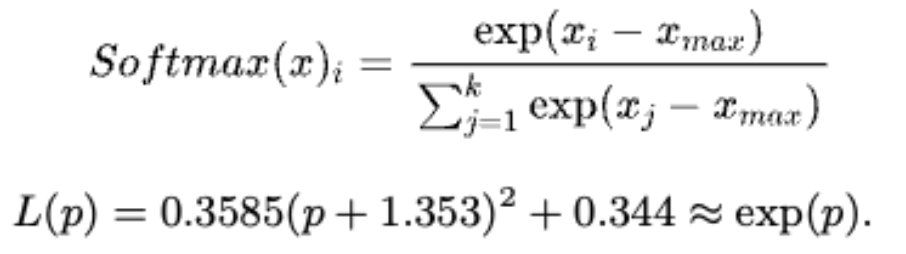
以上 GELU、SoftMax 的拟合实现都出自论文：I-BERT: Integer-only BERT Quantization

算子融合

算子融合(fuse)是将多个算子合并成一个，从而加速计算过程，也能一定程度减少量化误差，常见的融合组合有：

[conv, bn]、[conv, bn, relu]、[conv, relu]
[linear, relu]、[bn, relu]

这里举两个例子说明融合的计算过程：

1、conv + bn：

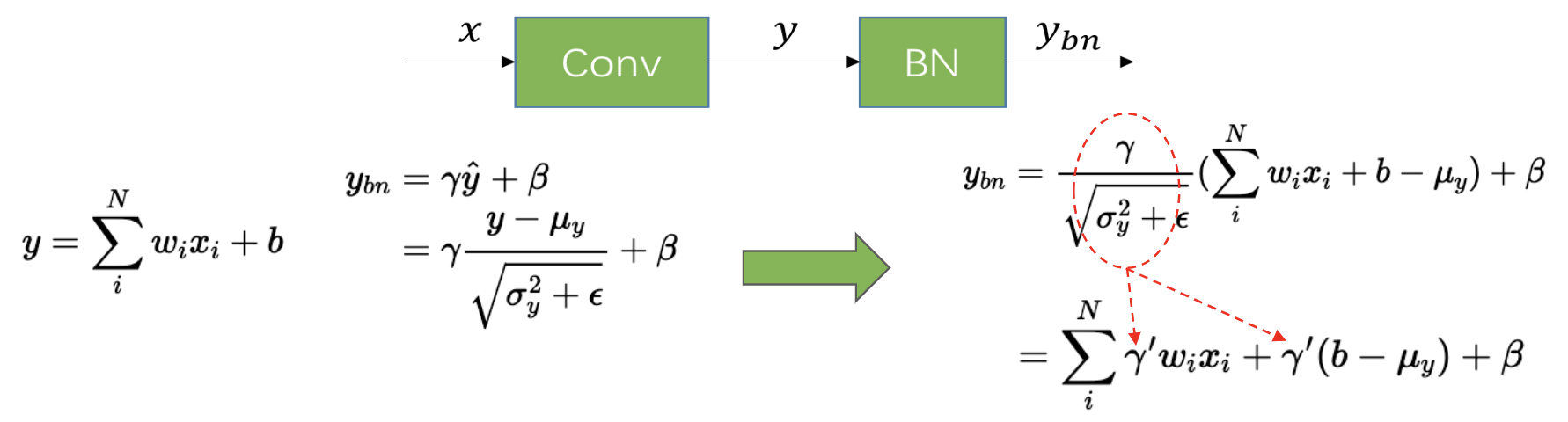
如上图，将 conv 公式展开到 bn 公式中，y_bn 最后也是一个 conv 的计算形式，因此 conv + bn 融合后仍然是一个 conv 算子

2、conv + relu：
relu 本质上是一个截断操作，可以通过clip实现，而量化计算本身就带了一个clip，因此可以并合并到之前的算子计算(linear，conv)

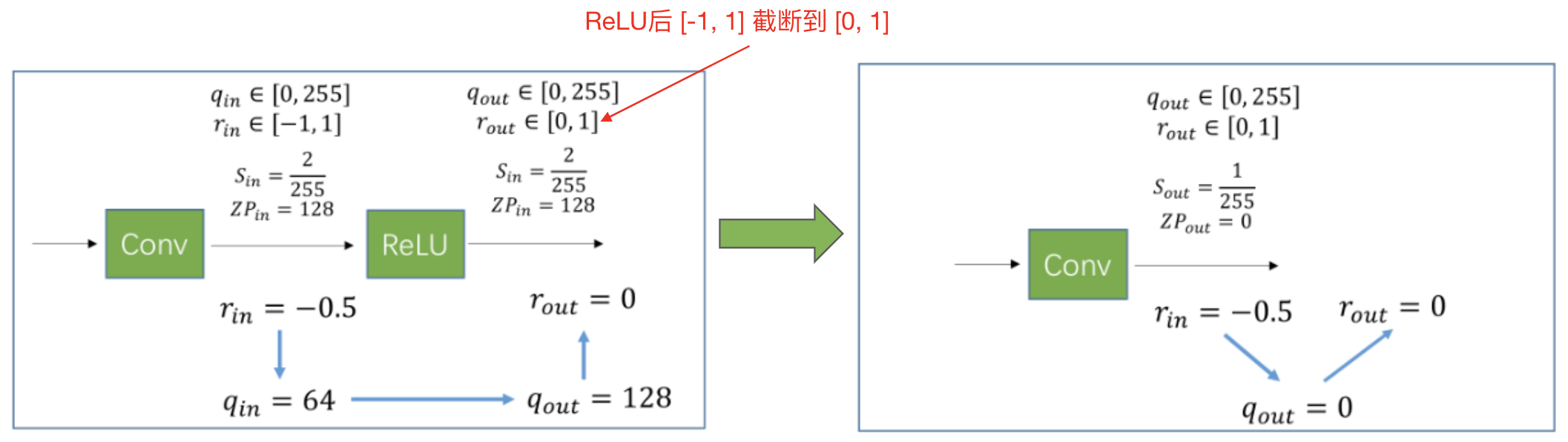
如上图 conv + relu 的融合后是还是一个 Conv，需要在 relu 后统计量化参数 (min-max)，就将 relu 的操作融合到了量化过程

其它优化

Ada Round

Ada Round 是高通提出的一种量化优化算法，其主要想法是：对conv中每个weight值进行量化时，不再是四舍五入的round-to-nearest，而是自适应的决定weight量化时将浮点值转到最近右定点值还是左定点值

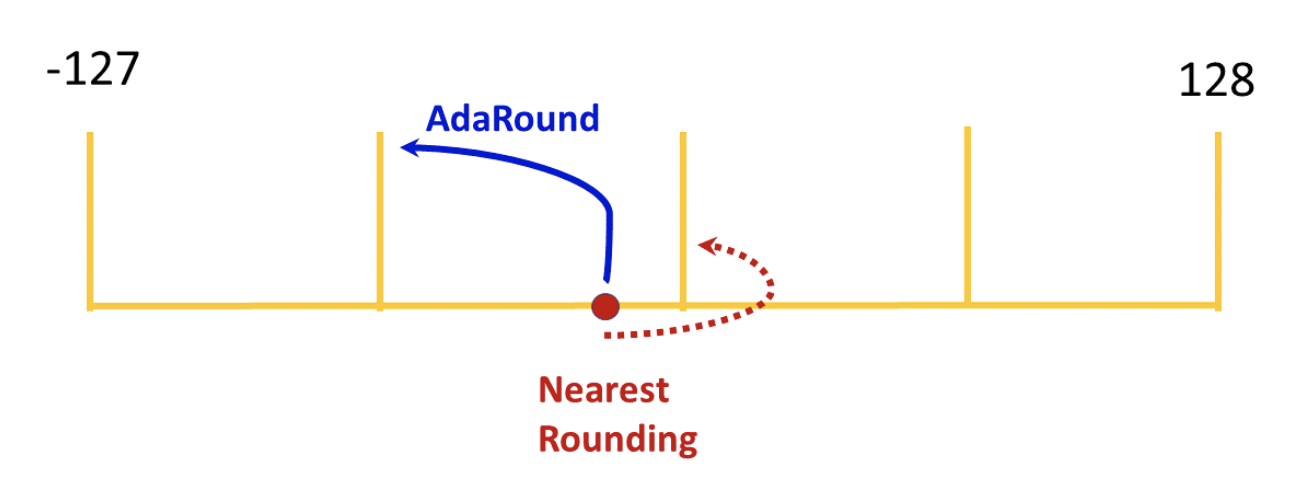
具体的算法实现比较复杂，详见论文: Up or Down? Adaptive Rounding for Post-Training Quantization

模型量化方法

模型的量化对象主要分权重和激活两类：

权重：训练完后固定，数值范围(range)与输入无关，可离线完成量化，通常相对容易量化；
激活：激活输出随输入变化而变化，需要统计数据动态范围，通常更难量化。范围统计的时机有两种：
- training：训练时进行统计
- calibration：训练后推理小批量数据进行统计

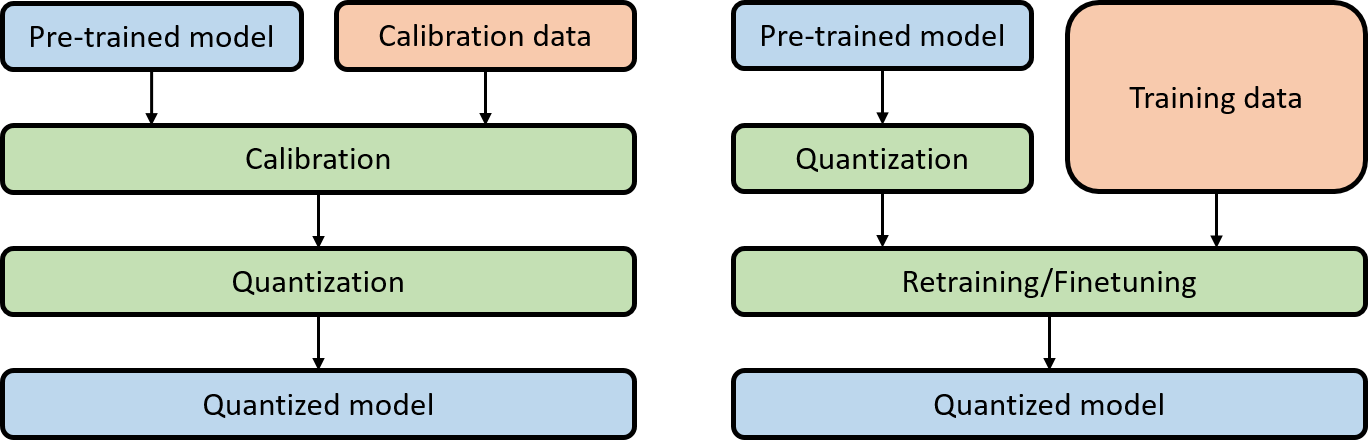
根据是否重新训练模型，量化方案主要分位两大类：

Post Training Quantization （PTQ）

训练后量化，相对简单高效，只需要已训练好的模型 + 少量校准数据，无需重新训练模型，根据是否量化激活又分为：
- Dynamic Quantization：仅量化权重，激活在推理时量化，无需校准数据
- Static Quantization：权重和激活都量化，需要校准数据
Quantization Aware Training（QAT）

量化感知训练：在模型中添加伪量化节点模拟量化，重新训练模型（finetune），流程相对复杂

PTQ dynamic

由于仅量化权重，也称为 weight-only quantization，其激活在推理时进行量化，适用于 LSTM、MLP、Transformer 等模型（权重参数量大）

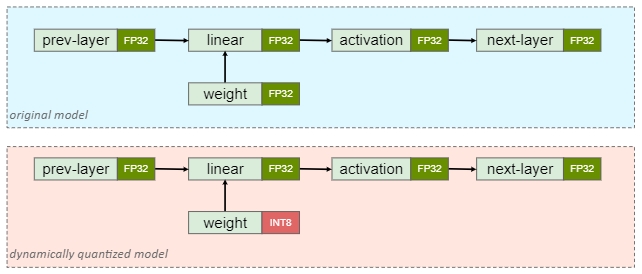
上图是 PTQ dynamic 模型量化前后的结构对比示意，即只有 weight 被提前量化成 INT8 ，下图是 NCNN 推理引擎中的实现，可以看到 conv 的计算是以 INT8 整型进行，为了避免溢出，内部的中间结果还是以 INT32 存储，然后反量化为 FP32 进行后续的计算。

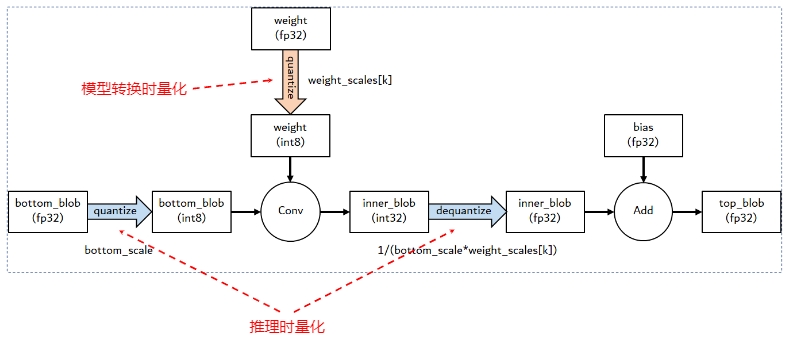
PTQ static

PTQ static 则是权重和激活都提前量化，为了量化激活，需要使用具有代表性的数据进行推理，然后统计各个激活的数据范围，这个步骤也称为“校准”(Calibration)。由于激活也量化了，通常会进行算子融合以提升性能

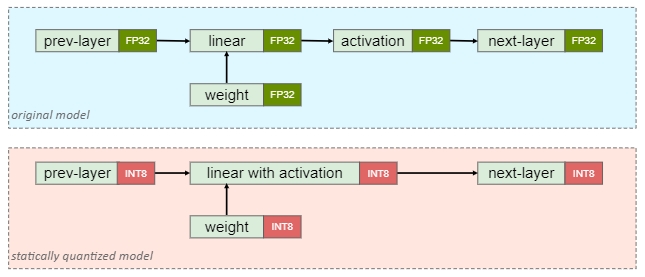
激活的数值范围统计决定了激活量化的精度，常用的方法有：

Min-Max

直接统计最小、最大值：
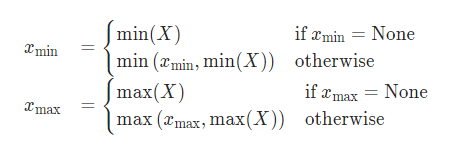
Moving Average Min-Max

增加了滑动平均，即当前的 min、max 与历史 min、max 的加权和
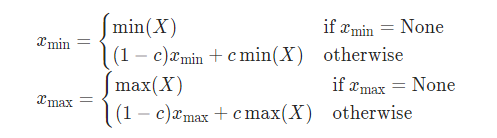
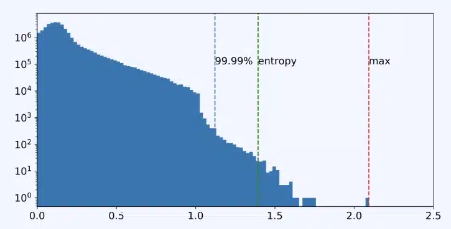
Histogram

统计数值分布直方图，然后基于最小化量化误差或 KL 散度等算法选择合适的范围，如下图，选择 [0, 1.5] 区间就能覆盖 99% 以上的值

QAT

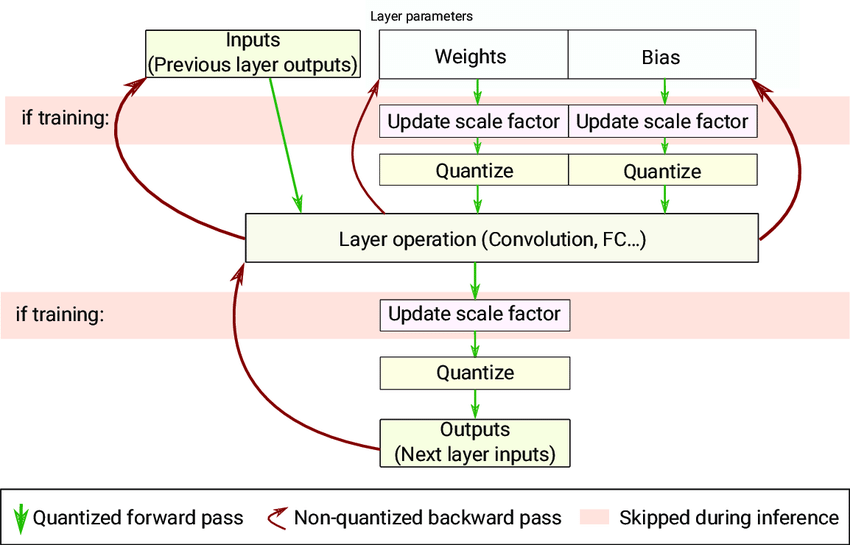
QAT 先在模型中添加伪量化节点，模拟量化过程，然后重新训练模型，通常可以获得更高精度

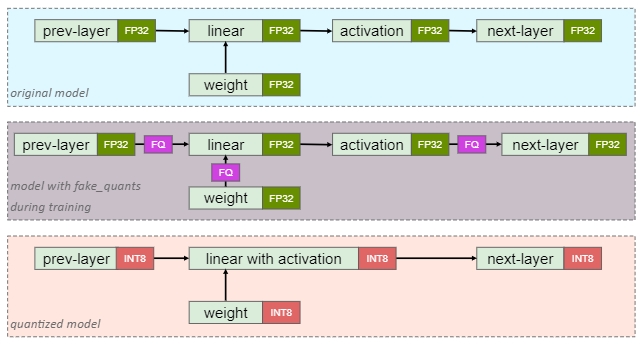
伪量化节点的功能有：

统计数据范围(如min-max)，更新量化参数(zero-point、scale)
对输入输出进行模拟量化（仍然表示为 FP32），从而让模型感知量化对结果的影响

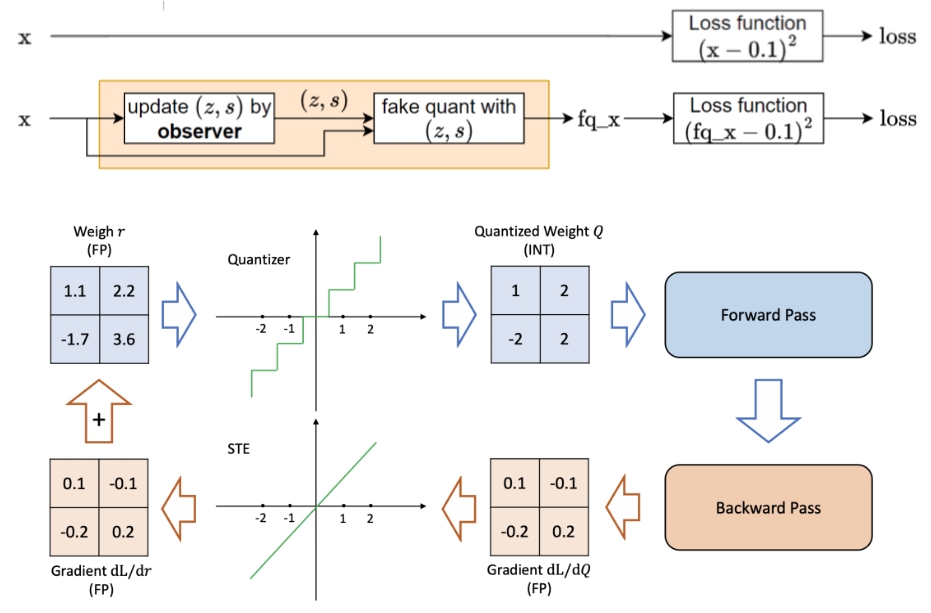
如上图，forward pass 过程中，伪量化节点 fq 的量化是一个阶梯型的函数，而在 backward pass 中，为了反向传播能正常进行，将 fq 的梯度计算设置为直通（STE），这样在 QAT 训练中，loss 就带上了量化影响，并且能正常进行梯度下降权重更新。下图是算子 QAT 过程的流程示意图：

方案对比

对比 PTQ(static) 和 QAT，其主要区别在于是否进行重新训练，PTQ 只需要少量校准数据，流程简单，而 QAT 需要插入伪量化节点重新训练/微调，流程更复杂，但精度通常也更高。

二、工程实践

如下图，模型量化的整体链路包括训练、量化、推理三部分，芯片厂商通常会提供针对自家芯片的量化工具/SDK，用于模型量化、格式转换、端侧部署等，如 NVIDIA、Intel、AMD、高通、华为、MTK 等

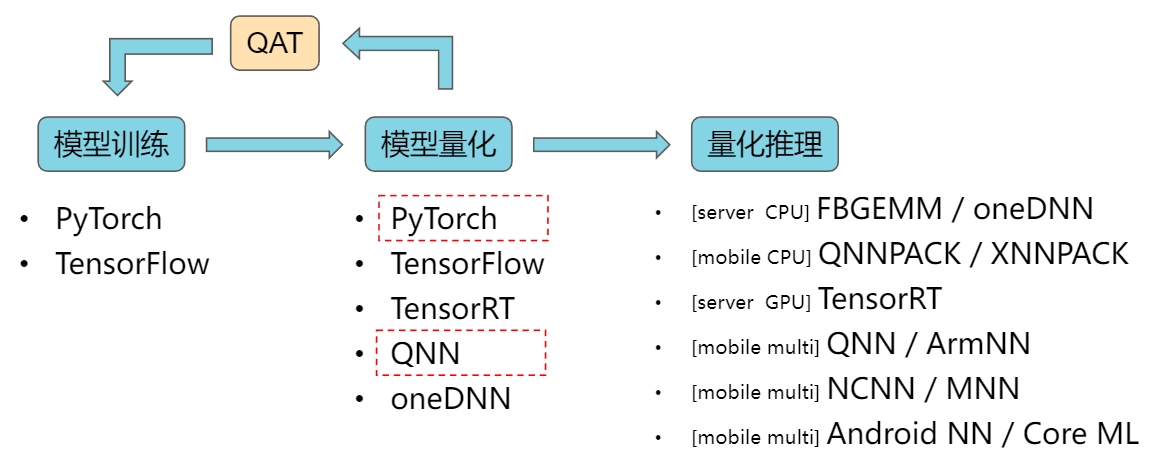
这里主要介绍红色框标注的 PyTorch 量化和高通 QNN 量化。

PyTorch 量化

目前的 PyTorch 2.x 版本对模型的量化提供了相对完善的支持，主要分为如下两种模式：

Eager Mode：手动模式，beta阶段，需要开发者改动较多
FX Graph Mode：全自动模式，prototype阶段，需要模型支持符号Trace

本文后面的示例都是 Eager Mode

基本概念

Quantized Tensor：已量化tensor，属性字段有：
- qscheme：量化模式，如 torch.per_tensor_affine、torch.per_channel_symmetric
- dtype：量化数据类型，如 torch.quint8、torch.qint8、torch.float16
- scale/per_channel_scales：量化参数 scale
- zero_point/per_channel_zero_points：量化参数 zero point
Observer：用于收集tensor的统计信息(如min、max)，并计算量化参数(S、Z)
FakeQuantize：模拟量化/反量化
QConfig：量化配置(权重、激活可分别配置)，可配置项包括：
- 不同类型的Observer、FakeQuantize
- dype
- qscheme
- quant_min/quant_max
Quantized Engine：量化执行引擎，如FBGEMM、QNNPACK等

PTQ dynamic

假如我们的模型 M 定义如下：

class M(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.fc = torch.nn.Linear(4, 4)

    def forward(self, x):
        x = self.fc(x)
        return x

PTQ dynamic 量化只需要调用 torch.ao.quantization.quantize_dynamic 方法即可：

model_fp32 = M()

model_int8 = torch.ao.quantization.quantize_dynamic(
    model_fp32,             # the original model
    {torch.nn.Linear},      # a set of layers to dynamically quantize
    dtype=torch.qint8)      # the target dtype for quantized weights

分别打印量化前后的模型如下：

model_fp32

M(
  (fc): Linear(in_features=4, out_features=4, bias=True)
)

model_int8

M(
  (fc): DynamicQuantizedLinear(in_features=4, out_features=4,
                               dtype=torch.qint8,
                               qscheme=torch.per_tensor_affine)
)

可以看到只是将浮点算子替换成了量化版本

PTQ static

为了量化激活，PTQ static 的步骤有：

1、模型中插入量化/反量化算子

class M(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.quant = torch.ao.quantization.QuantStub()
        self.conv = torch.nn.Conv2d(1, 1, 1)
        self.relu = torch.nn.ReLU()
        self.dequant = torch.ao.quantization.DeQuantStub()

    def forward(self, x):
        x = self.quant(x)
        x = self.conv(x)
        x = self.relu(x)
        x = self.dequant(x)
        return x

2、配置QConfig、配置算子融合

model_fp32 = M()
model_fp32.eval()
model_fp32.qconfig = torch.ao.quantization.get_default_qconfig('x86')
model_fp32_fused = torch.ao.quantization.fuse_modules(model_fp32, [['conv', 'relu']])

3、执行校准操作（输入校准数据进行推理）

model_fp32_prepared = torch.ao.quantization.prepare(model_fp32_fused)
input_fp32 = torch.randn(4, 1, 4, 4)
model_fp32_prepared(input_fp32)

4、转换为量化模型

model_int8 = torch.ao.quantization.convert(model_fp32_prepared)

同样地，我们可以打印中间步骤的模型结构：

model_fp32_prepared

M(
  (quant): QuantStub(
    (activation_post_process): HistogramObserver(min_val=-2.4940550327, max_val=3.4476957321))
  (conv): ConvReLU2d(
    (0): Conv2d(1, 1, kernel_size=(1, 1), stride=(1, 1))
    (1): ReLU()
    (activation_post_process): HistogramObserver(min_val=0.0, max_val=1.3560873270))
  (relu): Identity()
  (dequant): DeQuantStub()
)

可以看到，模型中增加了 QuantStub 和 DeQuantStub 用于量化/反量化，而 activation_post_process 则用于统计数值范围(这里是 HistogramObserver)，并且进行conv+relu融合后，之前的 relu 变成了 Identity()，而 conv 则变成了 ConvReLU2d

model_int8

M(
  (quant): Quantize(scale=tensor([0.0468]), zero_point=tensor([53]), dtype=torch.quint8)
  (conv): QuantizedConvReLU2d(1, 1, kernel_size=(1, 1), stride=(1, 1),
                                    scale=0.01067263912409544, zero_point=0)
  (relu): Identity()
  (dequant): DeQuantize()
)

量化为 int8 模型后，权重(conv)和激活(quant)节点都带上了量化系数 scale、zero_point，用于推理时的计算

QAT

PyTorch 的 QAT 步骤如下：

1、模型中插入量化/反量化算子

class M(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.quant = torch.ao.quantization.QuantStub()
        self.conv = torch.nn.Conv2d(1, 1, 1)
        self.relu = torch.nn.ReLU()
        self.dequant = torch.ao.quantization.DeQuantStub()

    def forward(self, x):
        x = self.quant(x)
        x = self.conv(x)
        x = self.relu(x)
        x = self.dequant(x)
        return x

2、配置QConfig、配置算子融合

model_fp32 = M()
model_fp32.eval()
model_fp32.qconfig = torch.ao.quantization.get_default_qat_qconfig('x86')
model_fp32_fused = torch.ao.quantization.fuse_modules(model_fp32, [['conv', 'relu']])

3、插入伪量化算子，进行QAT训练

model_fp32_prepared = torch.ao.quantization.prepare_qat(model_fp32_fused.train())
training_loop(model_fp32_prepared)

4、转换为量化模型

model_fp32_prepared.eval()
model_int8 = torch.ao.quantization.convert(model_fp32_prepared)

可以看到，对比 PTQ static 的区别主要是步骤3，调用 prepare_qat 插入伪量化算子，然后训练/微调，我们可以打印步骤3的模型结构如下：

model_fp32_prepared

M(
  (quant): QuantStub(
    (activation_post_process): FusedMovingAvgObsFakeQuantize(
      fake_quant_enabled=tensor([1]), observer_enabled=tensor([1]), scale=tensor([1.]), zero_point=tensor([0], dtype=torch.int32), dtype=torch.quint8, quant_min=0, quant_max=127, qscheme=torch.per_tensor_affine, reduce_range=True
      (activation_post_process): MovingAverageMinMaxObserver(min_val=inf, max_val=-inf)
    ))
  (conv): ConvReLU2d(
    1, 1, kernel_size=(1, 1), stride=(1, 1)
    (weight_fake_quant): FusedMovingAvgObsFakeQuantize(
      fake_quant_enabled=tensor([1]), observer_enabled=tensor([1]), scale=tensor([1.]), zero_point=tensor([0], dtype=torch.int32), dtype=torch.qint8, quant_min=-128, quant_max=127, qscheme=torch.per_channel_symmetric, reduce_range=False
      (activation_post_process): MovingAveragePerChannelMinMaxObserver(min_val=tensor([]), max_val=tensor([]))
    )
    (activation_post_process): FusedMovingAvgObsFakeQuantize(
      fake_quant_enabled=tensor([1]), observer_enabled=tensor([1]), scale=tensor([1.]), zero_point=tensor([0], dtype=torch.int32), dtype=torch.quint8, quant_min=0, quant_max=127, qscheme=torch.per_tensor_affine, reduce_range=True
      (activation_post_process): MovingAverageMinMaxObserver(min_val=inf, max_val=-inf)
    ))
  (relu): Identity()
  (dequant): DeQuantStub()
)

可以看到模型中插入了三个 FusedMovingAvgObsFakeQuantize 伪量化算子，分别对应 ConvReLU2d 算子的输入、权重、输出。

Pytorch Eager 模式的量化，对模型的修改有：

在 forward 中添加量化/反量化算子
对不支持量化的算子，修改为支持的版本，如 ReLU6 修改为 ReLU 或 Clip
对模型中的一些数值计算，修改为对应 module 算子调用（需要存储量化参数）

其中数值计算包括如 add、cat、mul 等，如下面示例中的 forward，需要对加法进行修改，才能统计加法的数值范围，进而计算量化参数

class ResidualBlock(nn.Module):
  def __init__(self, conv, shortcut):
    super(ResidualBlock, self).__init__()
    self.conv = conv
    self.shortcut = shortcut
    self.skip_add = nn.quantized.FloatFunctional()

    def forward(self, x):
    # return self.conv(x) + self.shortcut(x)
    return self.skip_add.add(self.conv(x), self.shortcut(x))

PyTorch 的 QAT 训的一些经验技巧：

从 FP32 预训练模型进行 QAT finetune，通常比直接训练量化模型精度更高
适当以更小的 lr 进行 QAT finetune
在适当的 epoch 冻结量化参数、冻结 BatchNorm 的均值和方差估计，提高稳定性

num_train_batches = 20

# QAT finetune
for nepoch in range(8):
    train_one_epoch(qat_model, criterion, optimizer, data_loader, torch.device('cpu'), num_train_batches)
    if nepoch > 3:
        # Freeze quantizer parameters
        qat_model.apply(torch.ao.quantization.disable_observer)
    if nepoch > 2:
        # Freeze batch norm mean and variance estimates
        qat_model.apply(torch.nn.intrinsic.qat.freeze_bn_stats)

最佳实践

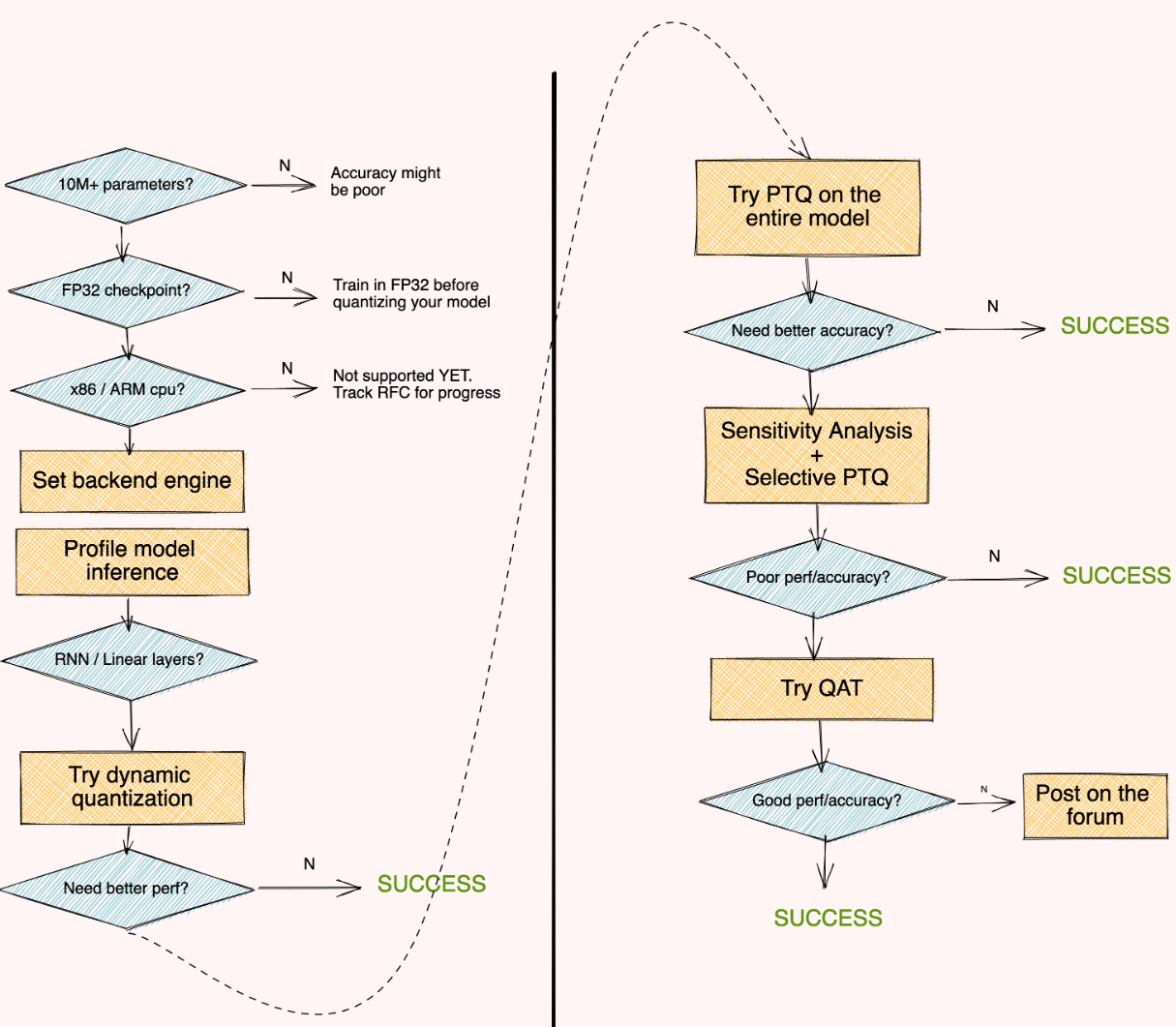
下图是 PyTorch 官方推荐的量化最佳实践，基本的原则是先尝试 PTQ，精度不足再尝试 QAT 和混合精度。

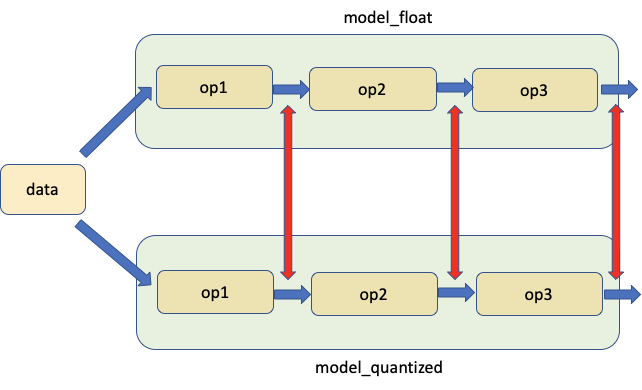
在对某层进行量化精度分析时，可以直接对比量化前后算子的输出差异（如余弦相似度）

高通 QNN 量化

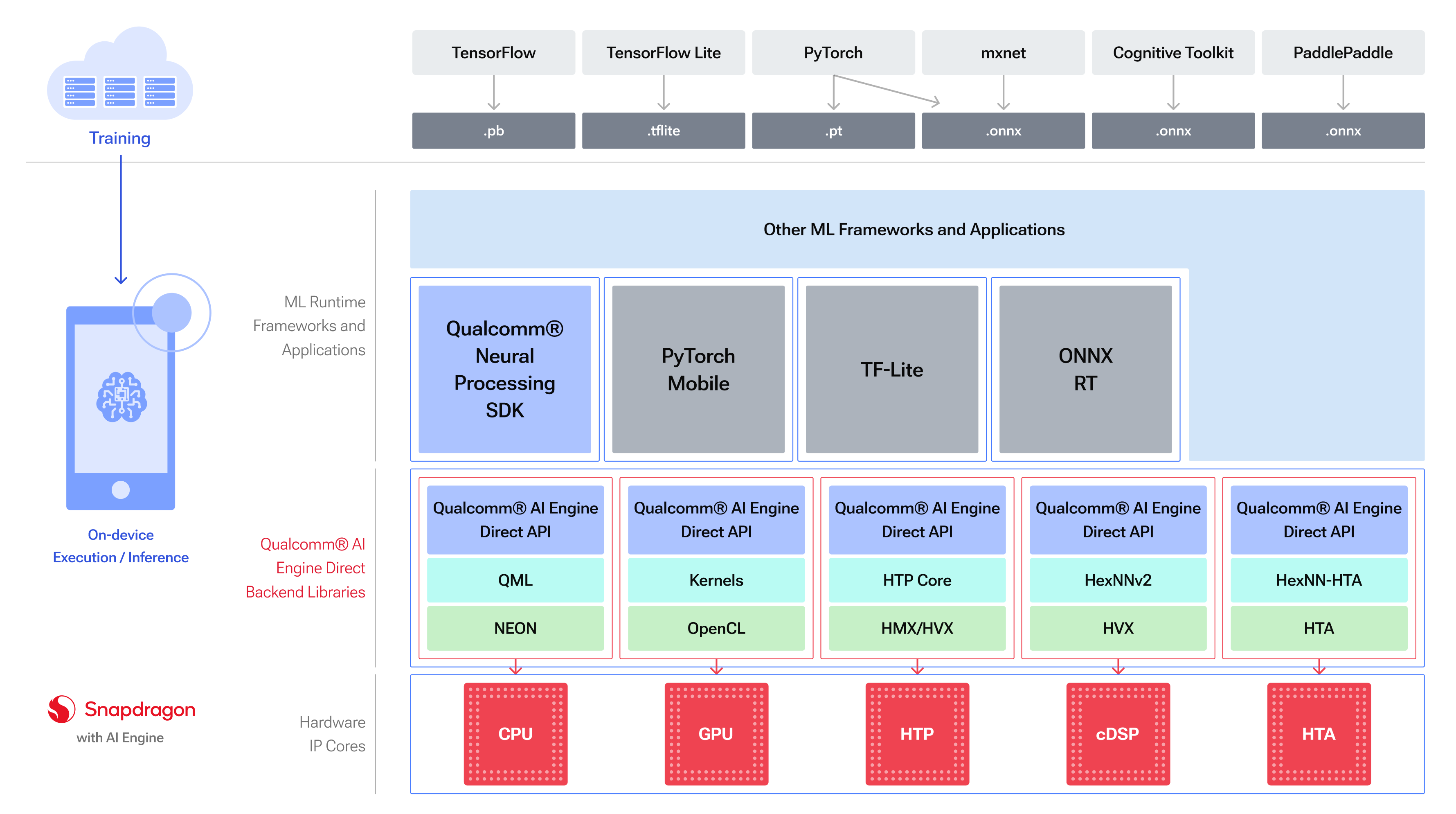
高通的 QNN 又名 Qualcomm® AI Engine Direct，是一个针对高通芯片的 AI 模型推理框架，完整文档可查看：https://docs.qualcomm.com/..

工具简介

QNN 支持将多种格式的模型转换为自有格式，然后运行在骁龙芯片的不同类型的 backend 上，如 CPU、GPU、HTP、DSP 等，骁龙8及以上支持的 HTP (Hexagon Tensor Processe) ，推理加速效果显著，实测相比CPU推理有5~10倍的性能提升。

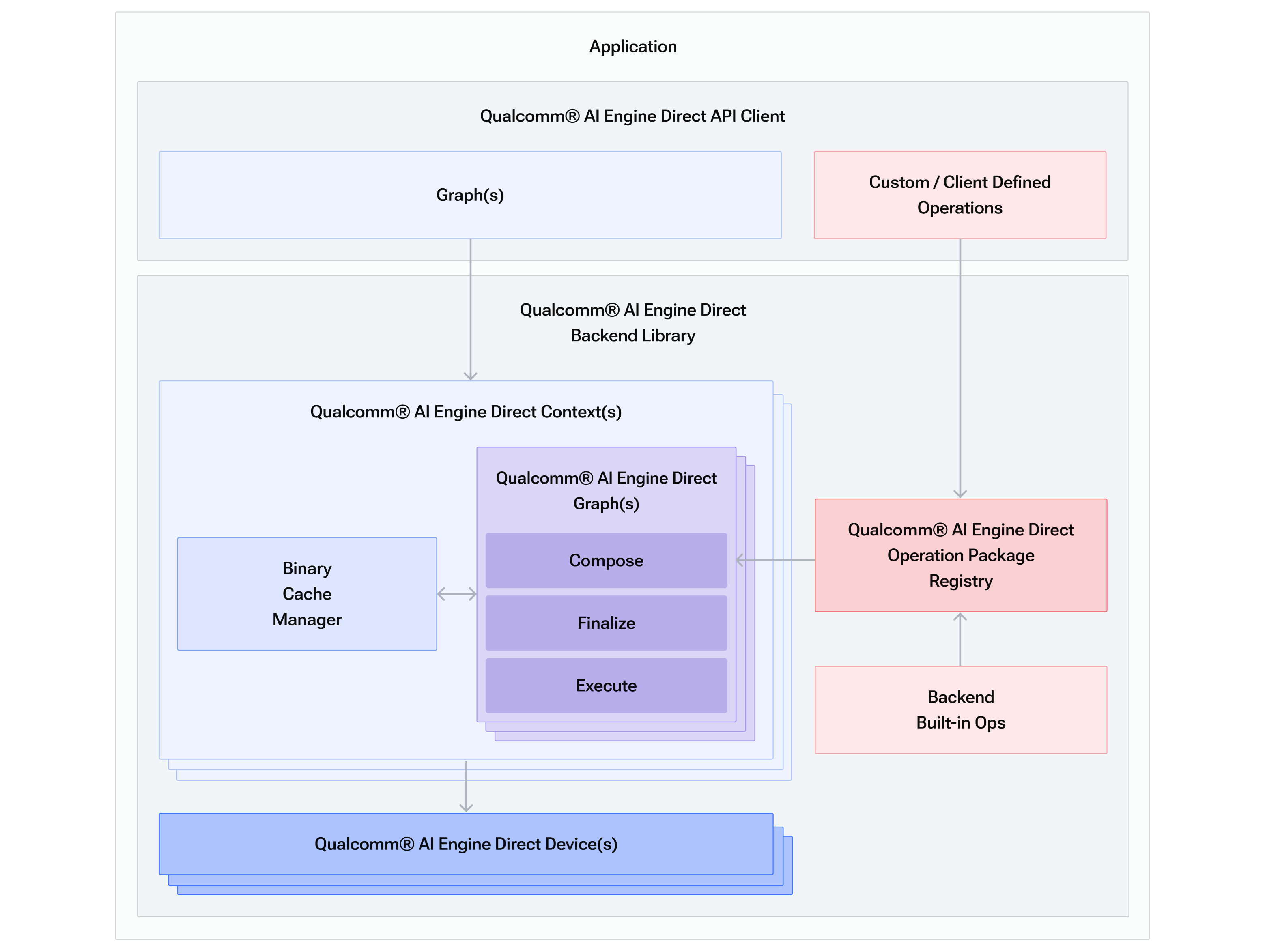
下图是 QNN 的逻辑架构，支持用户自定义算子，用户的AI模型转换为算子图结构(Graph)后，再基于实际的 backend上进行 Compose、Execute、Finalize，其中 Compose 后可以缓存起来，用于下次快速加载（类似于OpenGL/Vulkan的shader编译缓存）

然后是 QNN SDK 具体的工作流，左边是开发端的模型处理，右边是端侧的实际执行

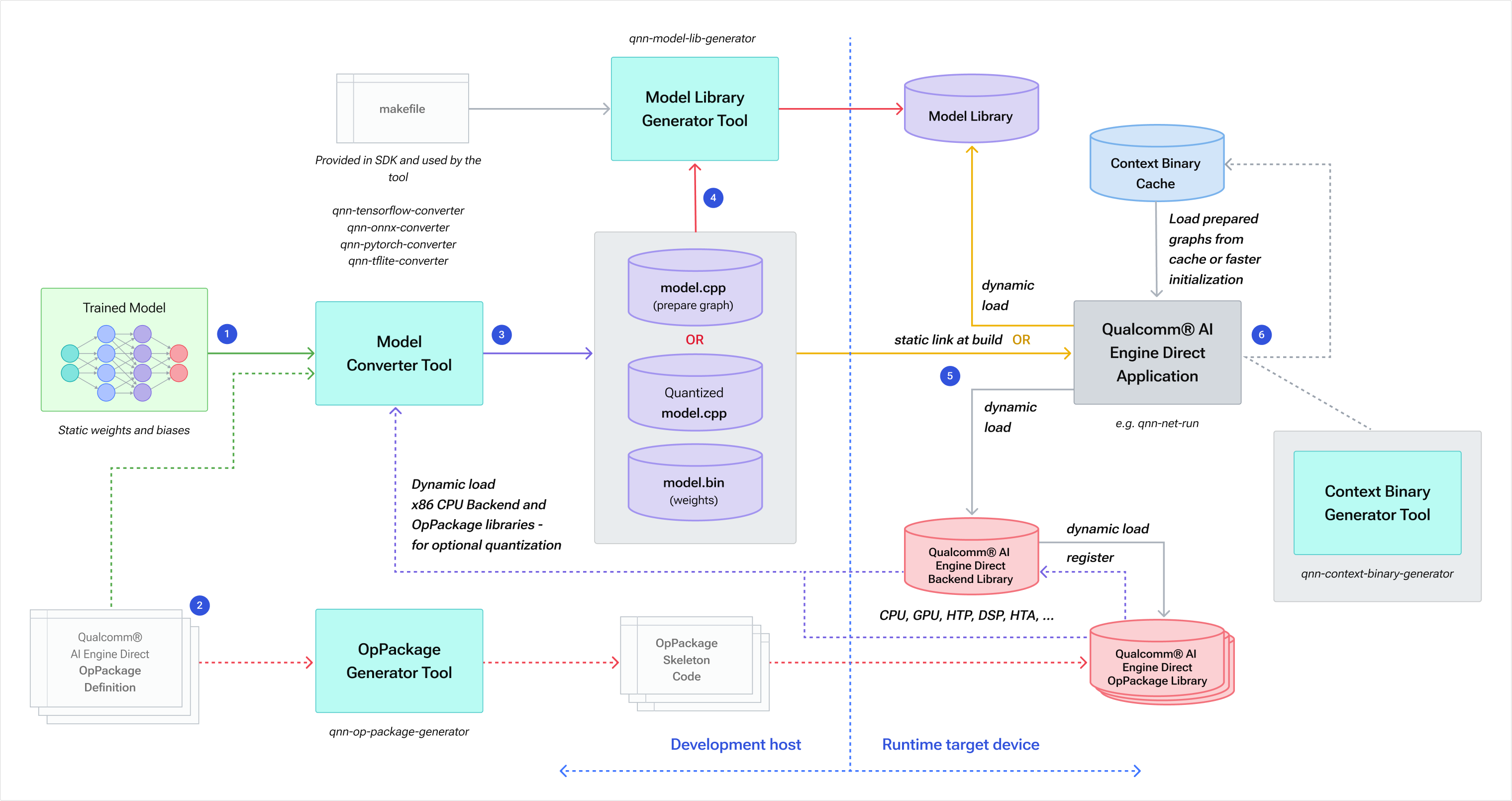
从这里可以看出整套工具链的一些特点：

算子包括 Skeleton 和 Stub 两部分，类似于接口和实现，不同的 backend 的有不同的 stub 实现；
用户模型拆分为图结构(.cpp)和权重(.bin)两个文件，.cpp 中同时包含了量化参数；
模型在具体的 backend 上可生成 Context Binary 缓存，下次可快速加载；

接下来我们看下具体的工具命令：

PTQ 示例

1、使用 converter 命令进行模型转换，得到 .cpp 和 .bin 文件，这里同时指定了量化参数和 PTQ 校准输入(–input_list)

${QNN_SDK_ROOT}/bin/x86_64-linux-clang/qnn-onnx-converter \
--input_network ${onnx_path} \
--input_list input_list_all.txt \
--act_bw 8 --weight_bw 8 --bias_bw 8 --param_quantizer symmetric \
--use_per_channel_quantization \
--output_path model_quant/my_model.quant.cpp

2、使用 generator 命令生成模型动态库，得到对应平台的 so 文件

${QNN_SDK_ROOT}/bin/x86_64-linux-clang/qnn-model-lib-generator \
-c model_quant/my_model.quant.cpp \
-b model_quant/my_model.quant.bin \
-o model_quant

3、使用 qnn-net-run 模拟运行（支持Linux/Android）

${QNN_SDK_ROOT}/bin/x86_64-linux-clang/qnn-net-run \
--backend ${QNN_SDK_ROOT}/lib/x86_64-linux-clang/libQnnHtp.so \
--model model_quant/x86_64-linux-clang/libmy_model.quant.so \
--input_list input_list_test.txt \
--output_dir output_quant

QAT 示例

QAT 与 PTQ 唯一区别在于模型转换时指定 quantization_overrides，这里 converter 逻辑可以理解为：计算权重、激活的量化参数时，优先使用 quantization_overrides 中指定的值，否则根据 input_list 校准数据进行推理&统计获得，即工具本身只能 PTQ，QAT 需要开发者导出量化参数后设置进来

${QNN_SDK_ROOT}/bin/x86_64-linux-clang/qnn-onnx-converter \
--input_network ${onnx_path} \
--input_list input_list_all.txt \
--act_bw 8 --weight_bw 8 --bias_bw 8 --param_quantizer symmetric \
--use_per_channel_quantization \
--quantization_overrides quantization_overrides.json \
--output_path model_quant/my_model.quant.cpp

quantization_overrides 需要开发者自行导出，比如经过 PyTorch 的 QAT 训练后的模型，导出 ONNX 后可以看到其中插入的量化/反量化节点，节点上的量化参数(scale、zero_point) 即是开发者需要导出的参数，按 QNN 规范写入 json 格式文件即可。

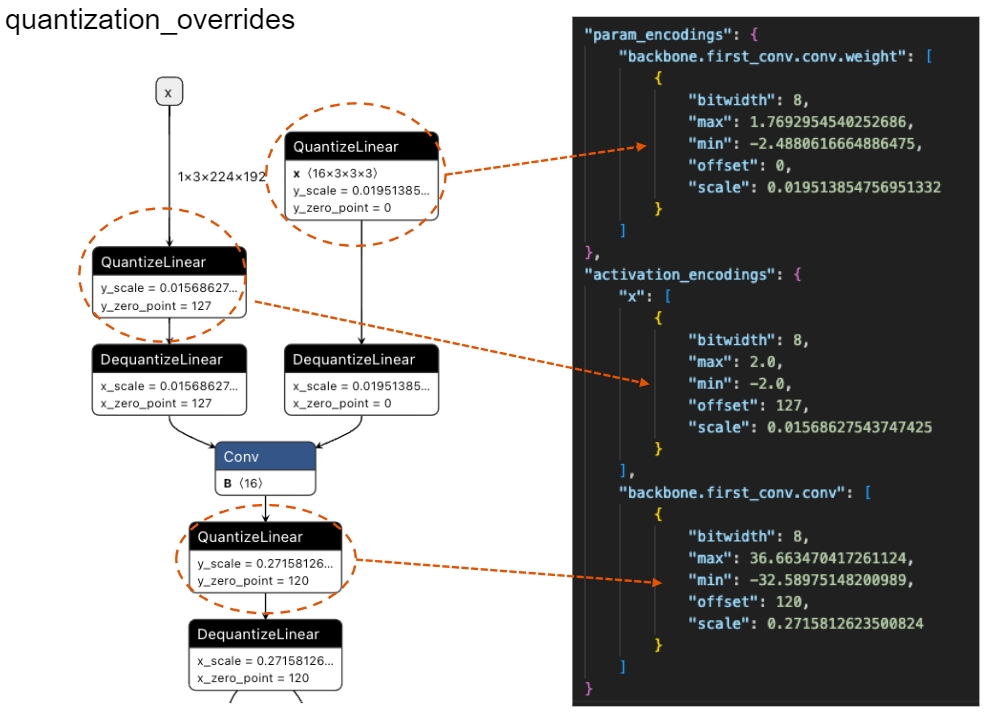
移动端部署

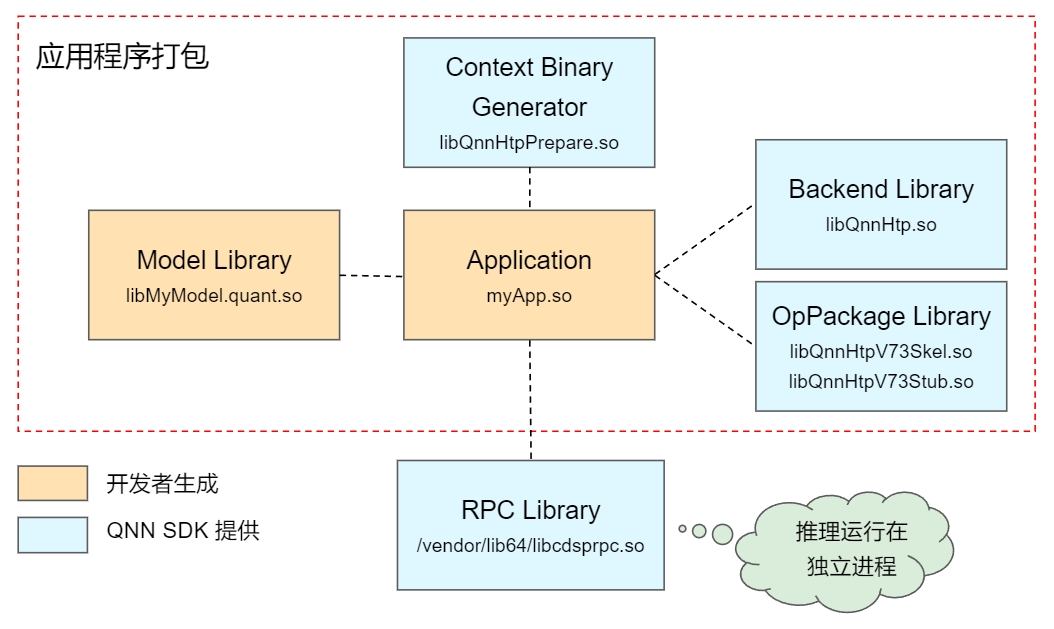
在使用工具完成模型的转换、生成后，移动端的部署如下图所示，开发者需要针对设备的硬件打包对应的库文件到 App 中，其中橙色部分为开发者生成，包括算法模型文件（基于.cpp、.bin生成）、整体调度逻辑 myApp.so，蓝色部分为 QNN SDK 提供的文件，包括 backend 实现库、算子库(Skel.so + Stub.so)、缓存生成库(Prepare.so)，以及内置在 Android 系统库中的 RPC 库(libcdsprpc.so)，需要 RPC 库的原因是 QNN 的推理都是在独立进程运行。

三、LLM 量化

针对 LLM 模型的量化是近年来研究的热点，基本原理与传统模型量化类似，但 LLM 模型有着自己的特点，比如参数量巨大，比如难以重新训练而主要是微调，这里介绍几个比较热门的 LLM 量化算法：

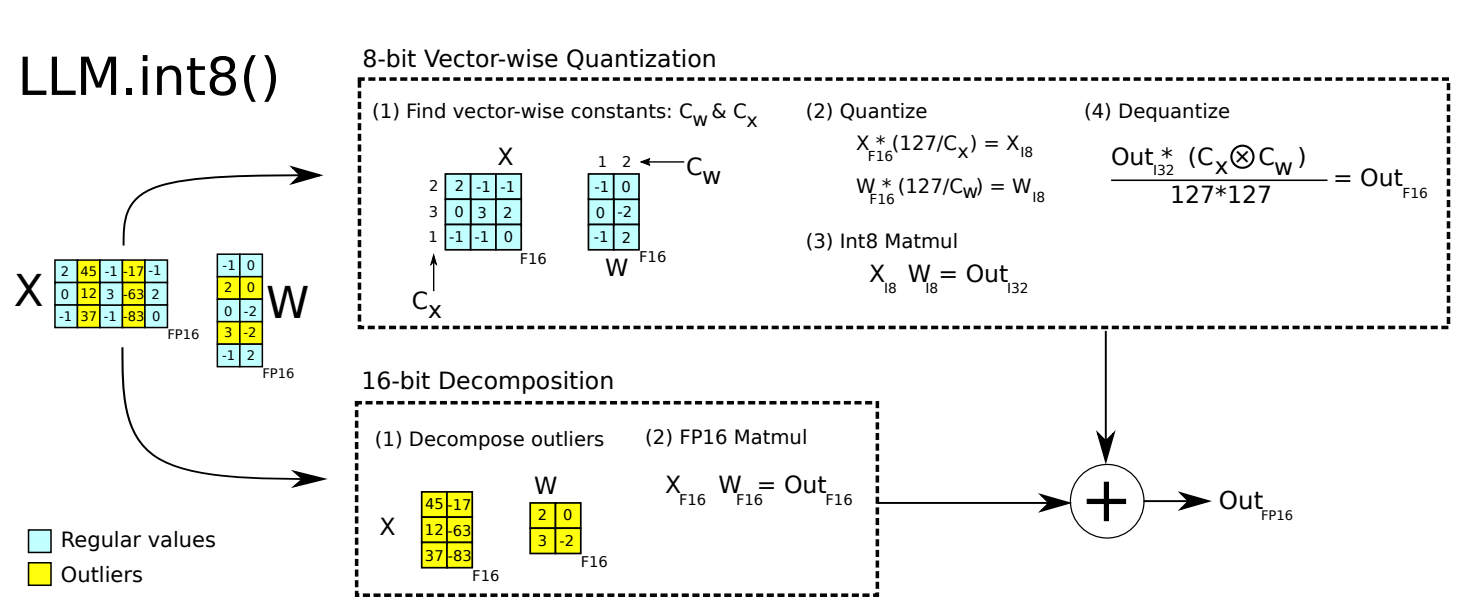
LLM.int8()

论文：https://arxiv.org/abs/2208.07339

LLM.int8() 主要是针对参数中的离群值(outliers) 进行处理：分析发现 outliers 主要分布在特定的几个维度，分离后用 FP16 乘法，其它维度用普通的 INT8 量化，最后把结果合并起来。整体上实现相对简单，精度高，但拆分、合并的过程对推理速度稍有影响。

SmoothQuant

论文：https://arxiv.org/abs/2211.10438

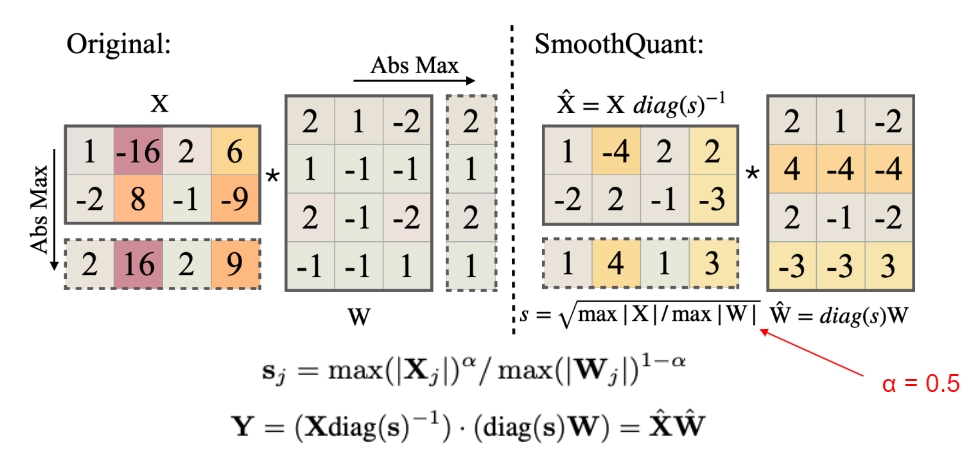
SmoothQuant 的核心思想是缩小激活，放大权重，使得激活更容易量化，通常来说由于各类 Norm 的存在，激活的波动范围会远大于权重，因此 SmoothQuant 从激活的参数中提取一个缩放系数，再乘到权重中，结果不变但压缩了激活的变换范围，从而减少了量化误差。

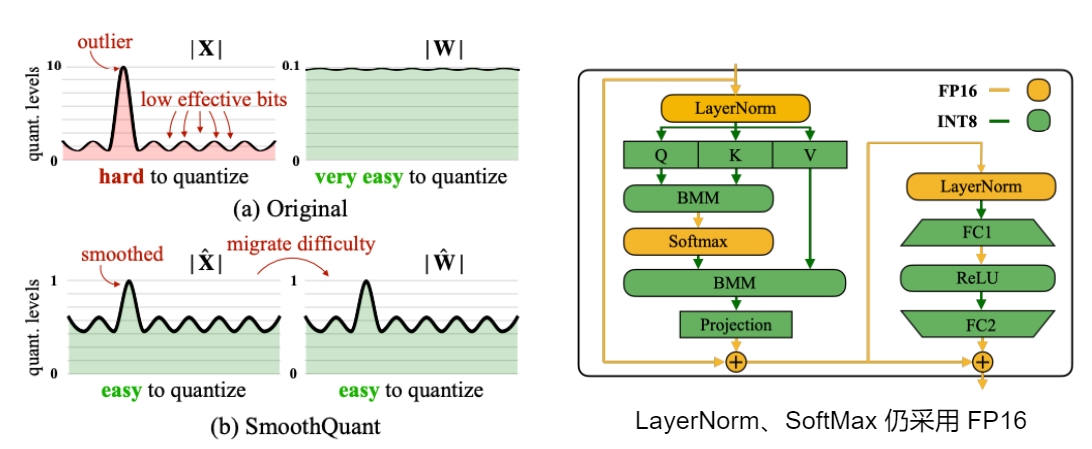
如下图是具体的计算示意，α 可以根据具体模型参数的分布进行调整。

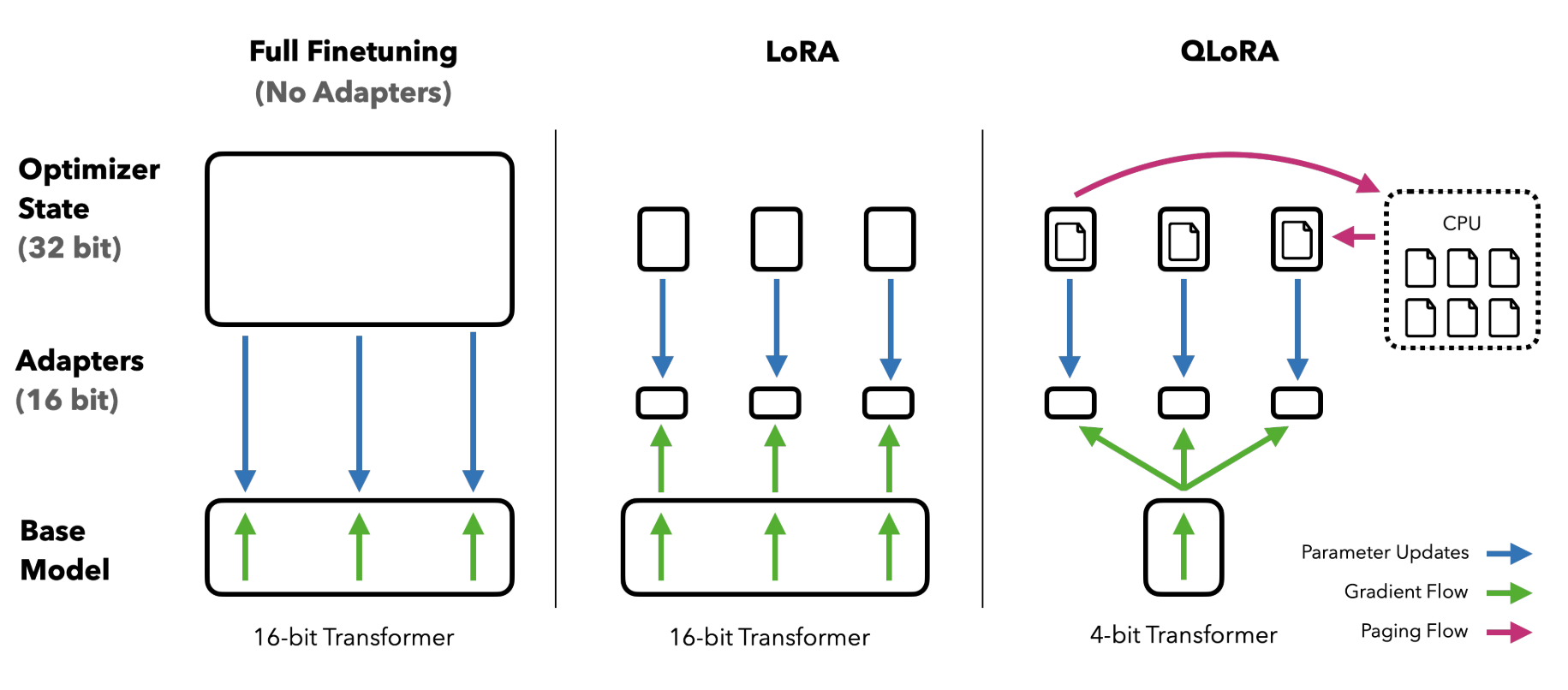
QLoRA

论文：https://arxiv.org/abs/2305.14314

LoRA 是大模型微调的重要方式，可以有效提升微调效率，而 QLoRA 则现对基础模型进行4-bit量化，显著降低了模型大小和显存要求，也就降低了 LLM 微调门槛

QLoRA 的量化/反量化计算逻辑如下：

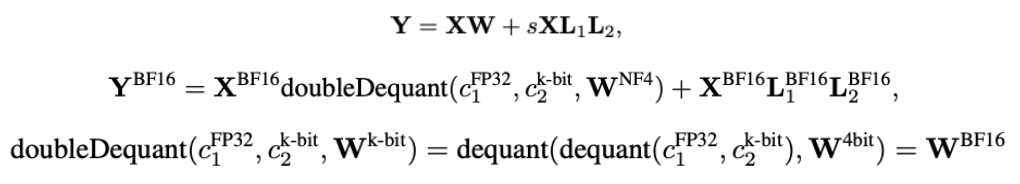
其主要有三个创新点：

使用 NF4 分位量化，本文前面原理部分已有详述
使用了双量化进一步减少模型大小：采用分块量化，每64个参数为一个block，共享归一化常数c2，然后每256块对c2进行 FP8 量化，这样每个参数的额外量化开销：8/64 + 32/(64 * 256) = 0.127 bit
基于 NVIDIA unified memory 实现分页优化器，GPU内存不足时使用CPU内存，进一步降低硬件要求

GPTQ

论文：https://arxiv.org/abs/2210.17323

GPTQ 与前面的量化方案都不一样，其主要想法是：从单层的角度考虑，找到一个量化过的权重，使得新老权重的输出差别最小：

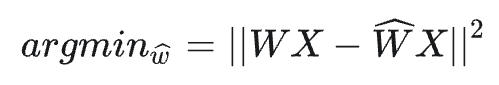
具体的迭代方案则是：对某个 block 内的所有参数逐个量化，每个参数量化后，适当调整这个 block 内其他未量化的参数，以弥补量化造成的精度损失，该算法由90年代的剪枝算法发展而来：

OBD (1990)：引入 H 矩阵进行神经网络剪枝
OBS (1993)：新增权重删除补偿
OBQ (2022)：将 OBS 应用到模型量化，并增加分行计算
GPTQ (2023)：进一步提升量化速度

具体的计算过程较为复杂，感兴趣的可以查阅上述相关论文。