October 28, 2016

参数标定即通过一定方法求得上述成像模型中的各个未知量(5个内参、6个外参以及畸变参数)。相机标定主要有传统标定方法和自标定方法两类,传统标定方法需要标定参照物,参照物的参数已知,然后分析拍摄到的参照物图像,求得相机参数,如直接线性变换(DLT)方法、Tsai两步标定法和张正友平面标定法等。传统方法操作相对复杂,但精度较高。
自标定方法不需要标定参照物,只需要多幅图像点的对应关系就能求解出相机参数,如基于无穷远平面、绝对二次曲面的自标定方法、基于Kruppa方程的自标定方法等。自标定方法灵活方便,但由于是非线性标定,精度和鲁棒性都不高。
这里主要介绍张正友平面标定法,其操作相对简单,且精度较高,实际应用中很常用。
论文原文:A Flexible New Technique forCamera Calibration
整个标定过程包括如下步骤:
-
打印一张棋盘格,把它贴在一个平面上,作为标定物。
-
通过调整标定物或摄像机的方向,为标定物拍摄一些不同方向的照片
-
从照片中提取棋盘格角点。
-
估算理想无畸变的情况下,五个内参和六个外参。
-
应用最小二乘法估算实际存在径向畸变下的畸变系数。
-
极大似然法,优化估计,提升估计精度。
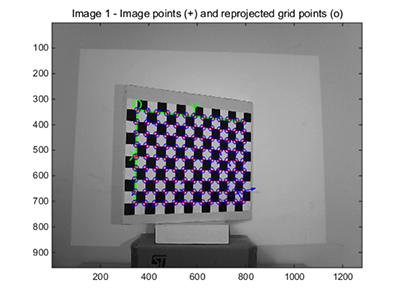
由于棋盘格上所有的角点都位于同一平面上,角点的世界坐标系的Z轴全部取0,即假定模板平面位于世界坐标系Z=0的平面上,因此,旋转矩阵减少一维,得到如下变换:
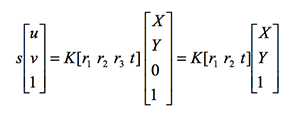
令 H=[h1 h2 h3]=K[r1 r2 t],H即为单应性矩阵,由旋转矩阵R正交性质,有:
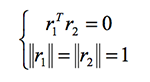
变换一下,可得约束方程:
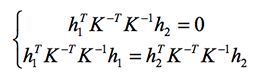
K中有5个未知变量,因此当拍摄3幅图像后,即可得3个H,在上述2个约束下可产生6个方程,就可以解出K的全部5个变量。再求得K后,可通过如下变换求得外参R、t:
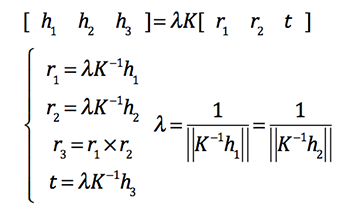
此时得到的内参K和外参[R|t]都是假设理想无畸变的情况,张正友标定法在此基础上,接着应用最小二乘法估计径向畸变系数,最后用极大似然法进行整体的估计优化。
实际应用中,常使用MATLAB标定工具箱进行相机标定 Camera Calibration Toolbox for Matlab,只需导入拍摄的棋盘格照片,输入一些参数,然后对每张照片选择棋盘区域,就可以自动完成整个标定过程,并得到可视化的标定结果。